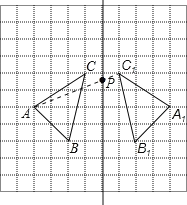
【题目】如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1,B与B1,C与C1相对应);
(2)求△ABC的面积;
(3)在直线l上找一点P,使得△PAC的周长最小.

参考答案:
【答案】(1)作图见解析;(2)5;(3)点P即为所求的点.
【解析】试题分析:(1)根据轴对称性作△ABC中顶点A,B,C关于直线l的对称点A1,B1,C1,然后再连接A1,B1,C1可得△A1B1C1,(2)利用割补法求△ABC的面积,利用过△ABC各顶点的矩形减去三个直角三角形的面积可求解,(3)要在直线l要上找到一点P,使△PAC周长最短,因为AC长为定值,所以要使△PAC周长最短,则使PA+PC的和最短,可作C关于直线l的对称点C1,连接A C1, 则A C1与直线l的交点即为所求的点P.
试题解析:(1)所作图形如图所示,
(2) ![]() ,所以△ABC的面积为5,
,所以△ABC的面积为5,
(3)连接A C1,则A C1与直线l的交点P即为所求的点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列根据等式的性质正确变形的是( ).
A.由- x=
x=  y,得x=2y
y,得x=2y
B.由3x-2=2x+2,得x=4
C.由2x-3=3x,得x=3
D.由3x-5=7,得3x=7-5 -
科目: 来源: 题型:
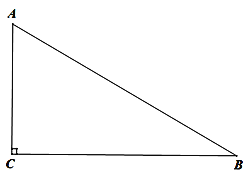
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠A>∠B.
(1)利用尺规作图在BC边上找一点P,使得点P到AB的距离等于PC的长度(不写作法,保留作图痕迹);
(2)在(1)的条件下,如果点P恰好又在线段AB的垂直平分线上,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】倒数等于本身的数是( )
A. 1 B. 0 C. -1 D. ±1
-
科目: 来源: 题型:
查看答案和解析>>【题目】节约用水,人人有责,某市为了鼓励居民节约用水,对自来水用户按如下标准收费:若每月每户用水不超过12吨,按每吨a元收费;若超过12吨,则超过部分按每吨2a元收费.如果小聪家六月份缴纳水费20a元,求小聪家这个月的实际用水量.
-
科目: 来源: 题型:
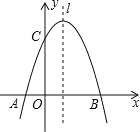
查看答案和解析>>【题目】如图,已知抛物线y=
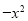 +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=
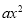 +bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;②当∠APB=120°时,a=
+bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;②当∠APB=120°时,a=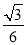 ;③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;④抛物线上存在点N,当△ABN为直角三角形时,有a≥
;③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;④抛物线上存在点N,当△ABN为直角三角形时,有a≥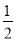 .正确的是( ).
.正确的是( ).A.①② B.③④ C.①②③ D.①②③④
相关试题

