Question

【题目】如图，抛物线y=ax2+2x﹣6与x轴交于点A（﹣6，0），B（点A在点B的左侧），与y轴交于点C，直线BD与抛物线交于点D，点D与点C关于该抛物线的对称轴对称．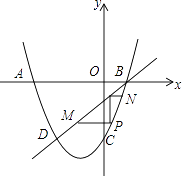

（1）连接CD，求抛物线的表达式和线段CD的长度；
（2）在线段BD下方的抛物线上有一点P，过点P作PM∥x轴，PN∥y轴，分别交BD于点M，N．当△MPN的面积最大时，求点P的坐标．

Answer 1

【答案】
（1）

解：将A点坐标代入函数解析式，得

36a﹣12﹣6=0．

解得a= ，

抛物线的解析式为y= x2+2x﹣6；

当x=0时y=﹣6．即C（0，﹣6）．

当y=﹣6时，﹣6= x2+2x﹣6，

解得x=0（舍），x=﹣4，即D（﹣4，﹣6）．

CD=0﹣（﹣4）=4，

线段CD的长为4；

（2）

解：如图

，

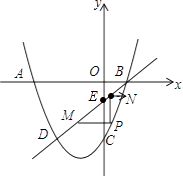当y=0时， x2+2x﹣6=0．解得x=﹣6（不符合题意，舍）或x=2．

即B（2，0）．

设BD的解析式为y=kx+b，将B、D点坐标代入函数解析式，得

，

解得 ，

BD的解析式为y=x﹣2，

当x=0时，y=﹣2，即E（0，﹣2）．

OB=OE=2，∠BOE=90°

∠OBE=∠OEB=45°．

∵点P作PM∥x轴，PN∥y轴，

∴∠PMN=∠PNM=45°，∠NPM=90°．

∵N在BD上，设N（a，a﹣2）；P在抛物线上，设P（a， a2+2a﹣6）．

PN=a﹣2﹣（ a2+2a﹣6）=﹣ a2﹣a+4=﹣ （a+1）2+ ，

S= PN2= [﹣ （a+1）2+ ]2，

当a=﹣1时，S最大= ×（ ）2= ，

a=﹣1， a2+2a﹣6=﹣ ，

点P的坐标为（﹣1，﹣ ）．

【解析】（1）根据待定系数法，可得函数解析式；根据自变量与函数值的对应关系，可得C、D点坐标，根据平行于x轴直线上两点间的距离是较大的小横坐标减较的横坐标，可得答案；（2）根据待定系数法，可得BD的解析式，根据自变量与函数值的对应关系，可得E点坐标，根据等腰三角形的性质，可得∠OBE=∠OEB=45°，根据平行线的性质，可得∠PMN=∠PNM=45°，根据直角三角形的判定，可得∠P，根据三角形的面积公式，根据二次函数的性质，可得a的值，再根据自变量与函数值的对应关系，可得答案．