【题目】在下面给出的数轴中,点 A 表示 1,点 B 表示-2,回答下面的问题:
(1)A、B 之间的距离是 ;
(2)观察数轴,与点 A 的距离为 5 的点表示的数是: ;
(3)若将数轴折叠,使点 A 与-3 表示的点重合,则点 B 与数 表示的点重合;
(4)若数轴上 M、N 两点之间的距离为 2018(M 在 N 的左侧),且 M、N 两点经过(3)中折 叠 后 互 相 重 合 , 则 M 、 N 两 点 表 示 的 数 分 别 是 : M : ;N: .
![]()
参考答案:
【答案】(1)3;(2)6或-4;(3)0;(4) M : -1010 ;N: 1008 .
【解析】
(1)(2)观察数轴,直接得出结论;
(3)A点与-3表示的点相距4单位,其对称点为-1,由此得出与B点重合的点;
(4)对称点为-1,M点在对称点左边,离对称点2018÷2=1009个单位,N点在对称点右边,离对称点1009个单位,由此求出M、N两点表示的数.
(1)A、B之间的距离是1+|2|=3.
故答案为:3;
(2)与点A的距离为5的点表示的数是:4或6.
故答案为:4或6;
(3)则A点与3重合,则对称点是1,则数B关于1的对称点是:0.
故答案为:0;
(4)由对称点为1,且M、N两点之间的距离为2018(M在N的左侧)可知,
M点表示数1010,N点表示数1008.
故答案为:1010,1008.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以线段AM为一边作正方形AMEF,连接FD.
(1)当点M在线段OD上时(如图1),线段BM与DF有怎样的数量及位置关系?请说明理由;
(2)当点M在线段OD的延长线上时(如图2),(1)中的结论是否仍然成立?请结合图2说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=x-2y,B=-x-4y+1.
(1)求2(A+B)-(A-B);(结果用含x,y的代数式表示)
(2)当
 与
与 互为相反数时,求(1)中代数式的值.
互为相反数时,求(1)中代数式的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】火车站、机场、邮局等场所都有为旅客提供打包服务的项目.现有一个长、宽、高分别为a、b 、30的箱子(其中a>b),准备采用如图①、②的两种打包方式,所用打包带的总长(不计接头处的长)分别记为
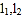 .
. 
(1)图①中打包带的总长
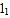 =________.
=________. 图②中打包带的总长
 =________.
=________.(2)试判断哪一种打包方式更节省材料,并说明理由.(提醒:先判断再说理,说理过程即为比较
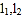 的大小.)
的大小.) (3)若b=40且a为正整数,在数轴上表示数
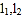 的两点之间有且只有19个整数点,求a 的值.
的两点之间有且只有19个整数点,求a 的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】规定:求若干个相同的有理数(均不等于 0)的除法运算叫做除方,如 2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等,类比有理数的乘方,我们把记作 2÷2÷2,2②,读作“2的圈 3 次方,”(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作:“(﹣3)的圈 4 次方”.一般地,把
 个
个 记作 a,读作 “a 的圈 n次方”
记作 a,读作 “a 的圈 n次方”(初步探究)
(1)直接写出计算结果:2②,(﹣
 )②.
)②.(深入思考)

我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
(2)试一试,仿照上面的算式,将下列运算结果直接写成幂的形式.
5⑥;(﹣
 )⑩.
)⑩.(3)想一想:有理数 a(a≠0)的圈n(n≥3)次方写成幂的形式等于多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(5分)某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负):

⑴根据记录可知前三天共生产________辆;
⑵产量最多的一天比产量最少的一天多生产________辆;
⑶该厂实行计件工资制,每辆车60元,超额完成任务每辆奖15元,少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中:
①由方程
 =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;②由方程
 x=
x= 两边同除以
两边同除以 ,得x=1;
,得x=1;③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣
 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
相关试题

