【题目】为了解学生的体能情况,随机选取了1000名学生进行调查,并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
项目 | 长跑 | 短跑 | 跳绳 | 跳远 |
200 | √ | × | √ | √ |
300 | × | √ | × | √ |
150 | √ | √ | √ | × |
200 | √ | × | √ | × |
150 | √ | × | × | × |
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大?
参考答案:
【答案】
(1)
解:同时喜欢短跑和跳绳的概率= ![]() =
= ![]() .
.
(2)
解:同时喜欢三个项目的概率= ![]() =
= ![]() .
.
(3)
解:同时喜欢短跑的概率= ![]() =
= ![]() ,同时喜欢跳绳的概率=
,同时喜欢跳绳的概率= ![]() =
= ![]() ,同时喜欢跳远的概率=
,同时喜欢跳远的概率= ![]() =
= ![]() ,
,
∵ ![]() ,
,
∴同时喜欢跳绳的可能性大
【解析】(1)根据求概率的公式即可得到结论;
(2)根据求概率的公式即可得到结论;
(3)根据求概率的公式求得各项概率进行比较即可得到结论. 本题考查了利用频率估计概率,求概率,正确的理解题意是解题的关键.
-
科目: 来源: 题型:
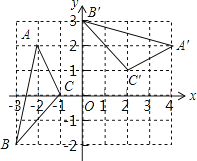
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
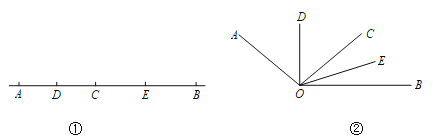
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于
 BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形. (1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4
 ,求∠C的大小.
,求∠C的大小.
-
科目: 来源: 题型:
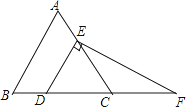
查看答案和解析>>【题目】在等边△ABC中,点D,E分别在边BC、AC上,若CD=2,过点D作DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

相关试题

