【题目】
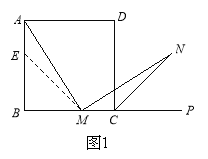
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
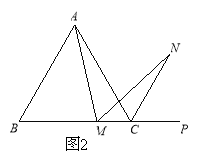
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
参考答案:
【答案】
(1)证明略
(2)理由略
(3)![]()
【解析】解:(1)∵AE=MC,∴BE=BM, ∴∠BEM=∠EMB=45°, ∴∠AEM=135°,
∵CN平分∠DCP,∴∠PCN=45°,∴∠AEM=∠MCN=135°
在△AEM和△MCN中:∵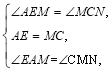 ∴△AEM≌△MCN,∴AM=MN
∴△AEM≌△MCN,∴AM=MN
(2)仍然成立.
在边AB上截取AE=MC,连接ME
∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=60°,
∴∠ACP=120°.
∵AE=MC,∴BE=BM
∴∠BEM=∠EMB=60°
∴∠AEM=120°.
∵CN平分∠ACP,∴∠PCN=60°,
∴∠AEM=∠MCN=120°
∵∠CMN=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠BAM
∴△AEM≌△MCN,∴AM=MN
(3)![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了支持国货,哈市某手机卖场计划用
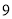 万元购进华为品牌手机.从卖场获知华为品牌
万元购进华为品牌手机.从卖场获知华为品牌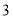 种不同型号的手机的进价及售价如下表:
种不同型号的手机的进价及售价如下表: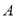 种
种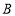 种
种 种
种进价(元/部)
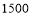
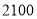
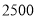
售价(元/部)
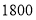
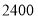
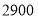
若该手机卖场同时购进两种不同型号的手机
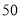 台,
台,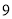 万元刚好用完.
万元刚好用完.(1)请您确定该手机的进货方案,并说明理由;
(2)该卖场老板准备把这批手机销售的利润
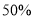 的捐给公益组织,在同时购进两种不同型号的手机方案中,为了使捐款最多,你选择哪种方案?
的捐给公益组织,在同时购进两种不同型号的手机方案中,为了使捐款最多,你选择哪种方案? -
科目: 来源: 题型:
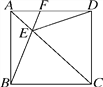
查看答案和解析>>【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
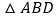 和
和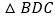 都是边长为1的等边三角形.
都是边长为1的等边三角形.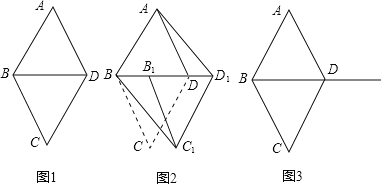
 四边形ABCD是菱形吗?为什么?
四边形ABCD是菱形吗?为什么? 如图2,将
如图2,将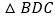 沿射线BD方向平移到
沿射线BD方向平移到 的位置,则四边形
的位置,则四边形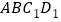 是平行四边形吗?为什么?
是平行四边形吗?为什么?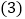 在
在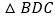 移动过程中,四边形
移动过程中,四边形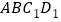 有可能是矩形吗?如果是,请求出点B移动的距离
有可能是矩形吗?如果是,请求出点B移动的距离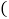 写出过程
写出过程 ;如果不是,请说明理由
;如果不是,请说明理由 图3供操作时使用
图3供操作时使用 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察:从2开始,连续的偶数相加,它们的和的情况如下图:

(1)当加数m的个数为n时,和(S)与n之间有什么样的数量关系,用公式表示出来;
(2)按此规律计算(写出必要的演算过程):
①2+4+6+…+300的值;
②162+164+166+…+400的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离是5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是( )
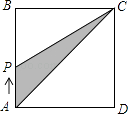
A.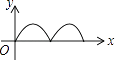
B.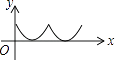
C.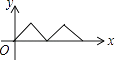
D.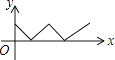
相关试题

