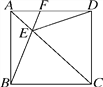
【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.
参考答案:
【答案】(1)见解析;(2)105°
【解析】试题分析:(1)根据正方形的性质可得BC=CD,∠ECB=∠ECD=45°,利用全等三角形的判定方法判定△BEC≌△DEC,(2)根据全等三角形的性质可得∠BEC=∠DEC= ![]() ,因为∠BED=120°,所以∠BEC=60°=∠AEF,
,因为∠BED=120°,所以∠BEC=60°=∠AEF,
所以∠EFD=60°+45°=105°.
试题解析: (1)证明:∵四边形ABCD是正方形,∴BC=CD,∠ECB=∠ECD=45°,
∴在△BEC与△DEC中,
 ,
,
∴△BEC≌△DEC(SAS),
(2)∵△BEC≌△DEC,
∴∠BEC=∠DEC= ![]() ,
,
∵∠BED=120°,
∴∠BEC=60°=∠AEF,
∴∠EFD=60°+45°=105°.
-
科目: 来源: 题型:
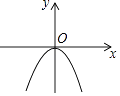
查看答案和解析>>【题目】已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a﹣1=0的根的存在情况是( )
A.没有实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确结论是( )
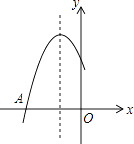
A.②④
B.①④
C.②③
D.①③ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.
(1)求证:OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其他条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
相关试题

