【题目】为了支持国货,哈市某手机卖场计划用![]() 万元购进华为品牌手机.从卖场获知华为品牌
万元购进华为品牌手机.从卖场获知华为品牌![]() 种不同型号的手机的进价及售价如下表:
种不同型号的手机的进价及售价如下表:
|
|
| |
进价(元/部) |
|
|
|
售价(元/部) |
|
|
|
若该手机卖场同时购进两种不同型号的手机![]() 台,
台,![]() 万元刚好用完.
万元刚好用完.
(1)请您确定该手机的进货方案,并说明理由;
(2)该卖场老板准备把这批手机销售的利润![]() 的捐给公益组织,在同时购进两种不同型号的手机方案中,为了使捐款最多,你选择哪种方案?
的捐给公益组织,在同时购进两种不同型号的手机方案中,为了使捐款最多,你选择哪种方案?
参考答案:
【答案】(1)有如下两种方案:方案①:购进![]() 种
种![]() 台,购进
台,购进![]() 种
种![]() 台;方案②:购进
台;方案②:购进![]() 种
种![]() 台,购进
台,购进![]() 种
种![]() 台;理由见解析;(2)选择方案②.
台;理由见解析;(2)选择方案②.
【解析】
(1) 分三种情况,根据总价90000元列方程解答;
(2)根据(1)分别求出两种方案的捐款额进行比较即可.
(1) ① 设购买![]() 种
种![]() 台,
台,![]() 种
种![]() 台,得
台,得
1500x+2100(50-x)=90000,
解得x=25,
∴50-x=25,
即购进![]() 种
种![]() 台,购进
台,购进![]() 种
种![]() 台.
台.
② 设购买![]() 种
种![]() 台,
台,![]() 种
种![]() 台,得
台,得
1500a+2500(50-a)=90000,
解得a=35,
∴50-a=15,
即购进![]() 种
种![]() 台,购进
台,购进![]() 种
种![]() 台.
台.
③ 设购买![]() 种
种![]() 台,
台,![]() 种
种![]() 台,得
台,得
2100m+2500(50-m)=90000,
![]()
![]()
不符合题意,故舍去.
综上所述,有如下两种方案:
方案①:购进![]() 种
种![]() 台,购进
台,购进![]() 种
种![]() 台;
台;
方案②:购进![]() 种
种![]() 台,购进
台,购进![]() 种
种![]() 台.
台.
(2) 方案①:
![]() 元,
元,![]() 元,
元,
方案②:
![]() 元,
元,![]() 元,
元,
∵7500<8250,
![]() 选择方案②.
选择方案②.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B(4、0)两点,与y轴交于C点.

(1)求抛物线的解析式;
(2)T是抛物线对称轴上的一点,且△ATC是以AC为底的等腰三角形,求点T的坐标;
(3)M、Q两点分别从A、B点以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到原点时,点Q立刻掉头并以每秒 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,过点M的直线l⊥x轴交AC或BC于点P.求点M的运动时间t与△APQ面积S的函数关系式,并求出S的最大值.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,过点M的直线l⊥x轴交AC或BC于点P.求点M的运动时间t与△APQ面积S的函数关系式,并求出S的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)如图,已知点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.
求证:(1)△ABC≌△DEF; (2)BE=CF

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象,目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会,乘客代表认为:公交公司应降低运营成本,实现扭亏,公交公司认为:运营成本难以下降,提高票价才能扭亏根据这两种意见,把图①分别改画成图②和图③.则下列判断不合理的是( )

A. 图①中点A的实际意义是公交公司运营后亏损1万元
B. 图①中点B的实际意义是乘客量为1.5万时公交公司收支平衡
C. 图②能反映公交公司意见
D. 图③能反映乘客意见
-
科目: 来源: 题型:
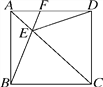
查看答案和解析>>【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
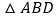 和
和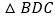 都是边长为1的等边三角形.
都是边长为1的等边三角形.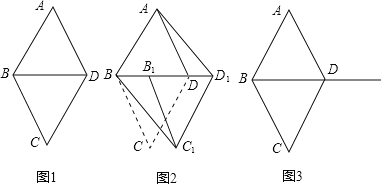
 四边形ABCD是菱形吗?为什么?
四边形ABCD是菱形吗?为什么? 如图2,将
如图2,将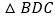 沿射线BD方向平移到
沿射线BD方向平移到 的位置,则四边形
的位置,则四边形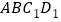 是平行四边形吗?为什么?
是平行四边形吗?为什么? 在
在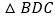 移动过程中,四边形
移动过程中,四边形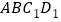 有可能是矩形吗?如果是,请求出点B移动的距离
有可能是矩形吗?如果是,请求出点B移动的距离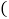 写出过程
写出过程 ;如果不是,请说明理由
;如果不是,请说明理由 图3供操作时使用
图3供操作时使用 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
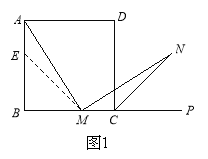
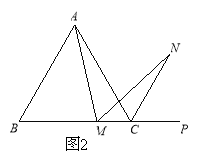
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正
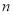 边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
相关试题

