【题目】如图,点A为平面直角坐标系第一象限内一点,直线y=x过点A,过点A作AD⊥y轴于点D,点B是y轴正半轴上一动点,连接AB,过点A作AC⊥AB交x轴于点C.
(1)如图,当点B在线段OD上时,求证:AB=AC;
(2)①如图,当点B在OD延长线上,且点C在x轴正半轴上, OA、OB、OC之间的数量关系为________(不用说明理由);
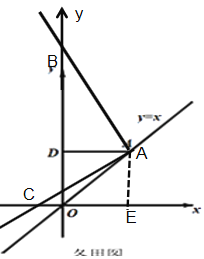
②当点B在OD延长线上,且点C在x轴负半轴上,写出OA、OB、OC之间的数量关系,并说明原因.
(3)直线BC分别与直线AD、直线y=x交于点E、F,若BE=5,CF=12,直接写出AB的长.

参考答案:
【答案】(1)证明见解析;(2)①OA=![]() (OC+OB);②OA=
(OC+OB);②OA=![]() (OB-OC);(3)10
(OB-OC);(3)10![]() ; 15
; 15![]() .
.
【解析】
(1)过点A作AE⊥OC于点E,先证明四边形ADOE是正方形,再证明Rt△ADB≌Rt△AEC(AAS),从而求得结论;(2)①过点A作AE⊥OC于点E,方法同(1)证明四边形ADOE是正方形,Rt△ADB≌Rt△AEC,△AOD是等腰直角三角形,再应用勾股定理即可得结论OA=![]() (OC+OB);②方法同①得结论:OA=
(OC+OB);②方法同①得结论:OA=![]() (OB-OC);(3)①当点B在线段OD上时,将△AFC绕点A顺时针旋转90°,AC与AB重合,变为△ABF′,连接EF′,证明∠EBF′=90°,由勾股定理得EF′=13,再证明△AEF≌△AEF′,所以EF= EF′=13,BF=EF-EB=13-5=8,BC=BF+FC=8+12=20,而△ABC是等腰直角三角形,所以AB=
(OB-OC);(3)①当点B在线段OD上时,将△AFC绕点A顺时针旋转90°,AC与AB重合,变为△ABF′,连接EF′,证明∠EBF′=90°,由勾股定理得EF′=13,再证明△AEF≌△AEF′,所以EF= EF′=13,BF=EF-EB=13-5=8,BC=BF+FC=8+12=20,而△ABC是等腰直角三角形,所以AB=![]() =10
=10![]() ; ②当点B在OD延长线上,且点C在x轴正半轴上时,方法同①,解得:AB=15
; ②当点B在OD延长线上,且点C在x轴正半轴上时,方法同①,解得:AB=15![]() ;③当点B在OD延长线上,且点C在x轴负半轴上时,方法同上,解得:AB=3
;③当点B在OD延长线上,且点C在x轴负半轴上时,方法同上,解得:AB=3![]() .
.
(1)过点A作AE⊥OC于点E,
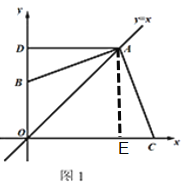
∵AD⊥y,点A在y=x上,∠DOE=90°
∴四边形ADOE是矩形,AE=OE,
∴矩形ADOE是正方形,
∴AD=AE,∠DAE=∠BAC=90°,
∴∠DAB=∠EAC,
又∵∠BDA=∠CEA=90°
∴Rt△ADB≌Rt△AEC
∴AB=AC.
(2)① 过点A作AE⊥OC于点E,
方法同(1)得,四边形ADOE是正方形,Rt△ADB≌Rt△AEC,AB=AC,BD=CE,
∴OC+OB=OC+OD+BD=OC+OD+CE=OE+OD=2OD,即OD=![]() (OC+OB)
(OC+OB)
又∵△AOD是等腰直角三角形,
∴由勾股定理得:OA=![]() OD =
OD =![]() ×
×![]() (OC+OB)=
(OC+OB)=![]() (OC+OB),
(OC+OB),
即OA=![]() (OC+OB),
(OC+OB),
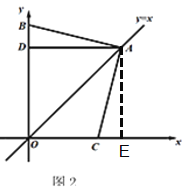
②过点A作AE⊥OC于点E,
方法同(1)得,四边形ADOE是正方形,Rt△ADB≌Rt△AEC,AB=AC,BD=CE,
∴OB-OD=OC+OE,即OB-OC=OD+OE=2OD=![]() OA,
OA,
又∵△AOD是等腰直角三角形,
∴由勾股定理得:OA=![]() OD,OD=
OD,OD= ![]() OA ,
OA ,
∴OB-OC= OD+OE=2OD=![]() OA,即OB-OC=
OA,即OB-OC=![]() OA,OA=
OA,OA=![]() (OB-OC)
(OB-OC)
(3)①当点B在线段OD上时,
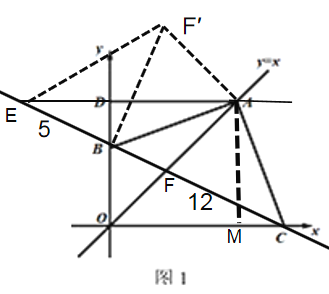
将△AFC绕点A顺时针旋转90°,AC与AB重合,变为△ABF′,连接EF′,BF′=CF=12,∠ACB=∠ABC=∠ABF′=45°,∠CBF′=∠ABC+∠ABF′=90°,所以∠EBF′=90°,
又∵BE=5,∴EF′=13,
∵∠F′AO=90°, ∠FAE=∠F′AE=45°,AE=AE,AF=AF′,
∴△AEF≌△AEF′
∴EF= EF′=13,BF=EF-EB=13-5=8,BC=BF+FC=8+12=20,
由(1)得:△ABC是等腰直角三角形,∴AB=![]() =10
=10![]() ;
;
②当点B在OD延长线上,且点C在x轴正半轴上时,
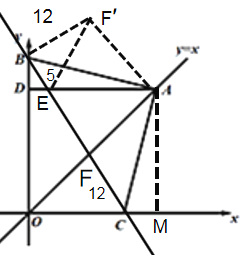
方法同①,旋转△AFC到△AF′B,证出∠EBF′,EF′=13=EF,BC=BE+EF+FC=5+13+12=30,所以等腰直角三角形ABC的直角边AB=15![]() ;
;
③当点B在OD延长线上,且点C在x轴负半轴上,
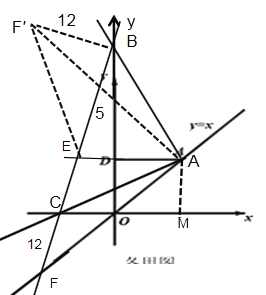
已证△ABC是等腰直角三角形,
过点B作BF′⊥BC于点B,截取 BF′=CF=12, 连接F′E、F′A,∵BE=5,
∴∠ABF′=∠ACF=135°,EF′=13
AB=AC,
∴△ABF′≌△ACF,可得AF′=AF,∠/span>BAF′=∠CAF,
∴∠BAC=∠F′AF=90°,
∵∠EAF=45°,
∴∠EAF=45°=∠EAF′,又AE=AE
∴△EAF≌△EAF′,
∴EF=EF′=13,EC=EF-CF=13-12=1,BC=BE+EC=1+5=6,
∴在等腰直角三角形ABC中,直角边AB=3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
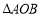 中,
中, ,将
,将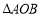 绕点
绕点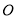 顺时针旋转
顺时针旋转 至
至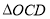 ,点
,点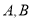 的对应点分别是
的对应点分别是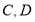 ,连接
,连接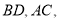 线段
线段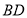 与线段
与线段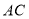 交于点M,连接
交于点M,连接 .
.(1)如图1,求证:
 ;
;(2)如图1,求证:OM平分
 ;
;(3)如图2,若
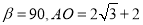 ,求
,求 的长.
的长.
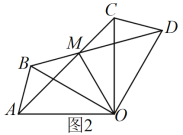
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.


(1)当直线MN绕点C旋转到图1的位置时,△ADC和△CEB全等吗?请说明理由.
(2)聪明的小亮发现,当直线MN绕点C旋转到图1的位置时,可得DE=AD+BE,请你说明其中的理由。
(3)小亮将直线MN绕点C旋转到图2的位置,线段DE、AD、BE之间存在着什么的数量关系,请写出这一关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在8×8的正方形网格中,每个小正方形的边长为1,△ABC的三个顶点均在格点上.
(1)将△ABC向右平移3个单位长度,再向下平移1个单位长度,画出对应图形△A′B′C′;
(2)写出A′、B′、C′坐标;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂共有120名生产工人,每个工人每天可生产螺栓25个或螺母20个,如果一个螺栓与两个螺母配成一套 ,那么每天安排多名工人生产螺栓,多少名工人生产螺母,才能使每天生产出来的产品配成最多套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
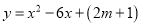 与x轴有交点.
与x轴有交点.(1)求m的取值范围;
(2)如果该二次函数的图像与x轴的交点分别为(x1,0),(x2,0),且2 x1 x2+ x1+ x2≥20,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC的顶点均在格点上,三个顶点的坐标分别是A(-3,4),B(-2,1),C(-4,2).
(1)将△ABC先向右平移7个单位长度,再向上平移2个单位长度,画出第二次平移后的△
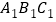 ;
;(2)以点O(0,0)为对称中心,画出与△ABC成中心对称的△
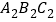 ;
;(3)将点B绕坐标原点逆时针方向旋转90°至点
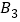 ,则点
,则点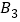 的坐标为(______,______)
的坐标为(______,______)
相关试题

