【题目】在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,点
,点![]() 的对应点分别是
的对应点分别是![]() ,连接
,连接![]() 线段
线段![]() 与线段
与线段![]() 交于点M,连接
交于点M,连接![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图1,求证:OM平分![]() ;
;
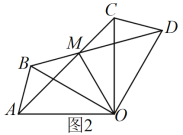
(3)如图2,若![]() ,求
,求![]() 的长.
的长.

参考答案:
【答案】(1)见详解;(2)见详解;(3)![]()
【解析】
(1)根据旋转的性质及OA=OB可得OA=OC=OB=OD,∠AOC=∠BOD,然后根据“SAS”证明△AOC≌△BOD即可得证;
(2)过点O作OE⊥AC,OF⊥BD,利用等积法可得OE=OF,再根据“HL”可证得Rt△MOE≌Rt△MOF即可得证;
(3)过点M作MH⊥AO,由![]() 可得∠OAC=∠ODB=45°,进而可证得△AOM≌△DOM,则∠MOD=∠MOA,利用
可得∠OAC=∠ODB=45°,进而可证得△AOM≌△DOM,则∠MOD=∠MOA,利用![]() 及
及![]() 可得∠MOA=60°,设OH=x,利用30°、45°的直角三角形的性质及勾股定理可表示出MO、MH、AH、AM的长,根据
可得∠MOA=60°,设OH=x,利用30°、45°的直角三角形的性质及勾股定理可表示出MO、MH、AH、AM的长,根据![]() 列出方程求解,进而可求得CM的长.
列出方程求解,进而可求得CM的长.
(1)证明:∵旋转,
∴OA=OC,OB=OD,∠AOC=∠BOD,
∵OA=OB,
∴OA=OC=OB=OD,
在△AOC与△BOD中,
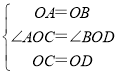
∴△AOC≌△BOD(SAS),
∴AC=BD;
(2)证明:过点O作OE⊥AC,OF⊥BD,垂足分别为E、F,
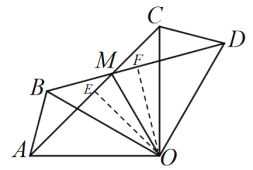
∵△AOC≌△BOD,
∴S△AOC=S△BOD,
∵OE⊥AC,OF⊥BD,
∴![]() ,
,
∵AC=BD,
∴OE=OF,
∵OE⊥AC,OF⊥BD,
∴∠MEO=∠MFO=90°,
在Rt△MOE与Rt△MOF中,
![]()
∴Rt△MOE≌Rt△MOF(HL),
∴∠OME=∠OMF,
∴OM平分![]() ;
;
(3)解:过点M作MH⊥AO,垂足为点H,
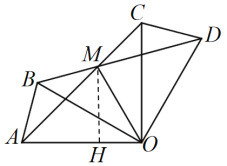
∵![]() ,OA=OC,OB=OD,
,OA=OC,OB=OD,
∴∠OAC=∠ODB=45°,
在△AOM与△DOM中,
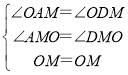
∴△AOM与△DOM(AAS),
∴∠AOM =∠DOM,
∵∠BOD=![]() ,∠AOB=30°,
,∠AOB=30°,
∴∠AOM =∠DOM=60°,
∵MH⊥AO,
∴∠MHO=∠MHA=90°,
∴在Rt△MHO中,∠OMH=30°,
设OH=x,则MO=2OH=2x,
∴![]() ,
,
∴在Rt△MHA中,∠HAM=45°,
∴AH=MH=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
解得:x=2,
∴![]() ,
,
在Rt△AOC中,![]() ,
,
∴![]() ,
,
∴CM的长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了全面推进素质教育,增强学生体质,丰富校园文化生活,高新区某校将举行春季特色运动会,需购买A,B两种奖品.经市场调查,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品1件和B种奖品3件,共需55元.
(1)求A、B两种奖品的单价各是多少元;
(2)运动会组委会计划购买A、B两种奖品共100件,购买费用不超过1160元,且A种奖品的数量不大于B种奖品数量的3倍,运动会组委会共有几种购买方案?
(3)在第(2)问的条件下,设计出购买奖品总费用最少的方案,并求出最小总费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:(有指定方法必须用指定方法)
(1)
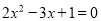 (配方法); (2)
(配方法); (2)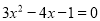 (公式法)
(公式法)(3)
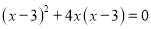 . (4)
. (4) .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,AB=AC,BC=12厘米,点D为AB上一点且BD=8厘米,点P在线段BC上以2厘米/秒的速度由B点向C点运动,设运动时间为t,同时,点Q在线段CA上由C点向A点运动.

(1)用含t的式子表示PC的长为_______________;
(2)若点Q的运动速度与点p的运动速度相等,当t=2时,三角形BPD与三角形CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,请求出点Q的运动速度是多少时,能够使三角形BPD与三角形CQP全等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.


(1)当直线MN绕点C旋转到图1的位置时,△ADC和△CEB全等吗?请说明理由.
(2)聪明的小亮发现,当直线MN绕点C旋转到图1的位置时,可得DE=AD+BE,请你说明其中的理由。
(3)小亮将直线MN绕点C旋转到图2的位置,线段DE、AD、BE之间存在着什么的数量关系,请写出这一关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在8×8的正方形网格中,每个小正方形的边长为1,△ABC的三个顶点均在格点上.
(1)将△ABC向右平移3个单位长度,再向下平移1个单位长度,画出对应图形△A′B′C′;
(2)写出A′、B′、C′坐标;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A为平面直角坐标系第一象限内一点,直线y=x过点A,过点A作AD⊥y轴于点D,点B是y轴正半轴上一动点,连接AB,过点A作AC⊥AB交x轴于点C.
(1)如图,当点B在线段OD上时,求证:AB=AC;
(2)①如图,当点B在OD延长线上,且点C在x轴正半轴上, OA、OB、OC之间的数量关系为________(不用说明理由);
②当点B在OD延长线上,且点C在x轴负半轴上,写出OA、OB、OC之间的数量关系,并说明原因.
(3)直线BC分别与直线AD、直线y=x交于点E、F,若BE=5,CF=12,直接写出AB的长.

相关试题

