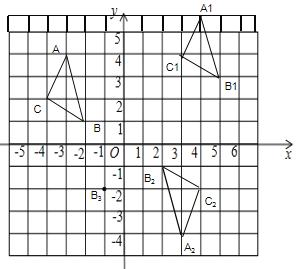
【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC的顶点均在格点上,三个顶点的坐标分别是A(-3,4),B(-2,1),C(-4,2).
(1)将△ABC先向右平移7个单位长度,再向上平移2个单位长度,画出第二次平移后的△![]() ;
;
(2)以点O(0,0)为对称中心,画出与△ABC成中心对称的△![]() ;
;
(3)将点B绕坐标原点逆时针方向旋转90°至点![]() ,则点
,则点![]() 的坐标为(______,______)
的坐标为(______,______)

参考答案:
【答案】(1)图形见解析;(2)图形见解析;(3)点B3见解析,B3的坐标为:(-1,-2).
【解析】
(1) (1)根据△ABC先向右平移7个单位长度,再向上平移2个单位长度,得出对应点坐标进而得出答案;
(2)根据△ABC关于原点O对称的△A2B2C2,得出对应点坐标进而得出答案;
(3)根据点B绕坐标原点逆时针旋转90°后所得的图形B3,得出对应点坐标进而得出答案.
解:(1)如图所示:△A1B1C1为所求;
(2)如图所示:△A2B2C2为所求;
(3)如图所示:点 B3即为所求,B3的坐标为:(-1,-2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A为平面直角坐标系第一象限内一点,直线y=x过点A,过点A作AD⊥y轴于点D,点B是y轴正半轴上一动点,连接AB,过点A作AC⊥AB交x轴于点C.
(1)如图,当点B在线段OD上时,求证:AB=AC;
(2)①如图,当点B在OD延长线上,且点C在x轴正半轴上, OA、OB、OC之间的数量关系为________(不用说明理由);
②当点B在OD延长线上,且点C在x轴负半轴上,写出OA、OB、OC之间的数量关系,并说明原因.
(3)直线BC分别与直线AD、直线y=x交于点E、F,若BE=5,CF=12,直接写出AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂共有120名生产工人,每个工人每天可生产螺栓25个或螺母20个,如果一个螺栓与两个螺母配成一套 ,那么每天安排多名工人生产螺栓,多少名工人生产螺母,才能使每天生产出来的产品配成最多套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
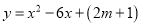 与x轴有交点.
与x轴有交点.(1)求m的取值范围;
(2)如果该二次函数的图像与x轴的交点分别为(x1,0),(x2,0),且2 x1 x2+ x1+ x2≥20,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)将下表填写完整:
平均数
中位数
方差
甲
8
乙
8
2
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 .(填“变大”或“变小”或“不变”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋中,放有三个标号分别为1,2,3的质地、大小都相同的小球.任意摸出一个小球,记为x,再从剩余的球中任意摸出一个小球,又记为y,得到点(x,y).
(1)用画树状图或列表等方法求出点(x,y)的所有可能情况;
(2)求点(x,y)在二次函数y=ax2﹣4ax+c(a≠0)图象的对称轴上的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC的平分线与BC的中垂线DE交于点E,过点E作AC边的垂线,垂足为N,过点E作AB延长线的垂线,垂足为M.
(1)求证:BM=CN;
(2)若,AB=2,AC=8,求BM的长.

相关试题

