【题目】关于x的一元二次方程(m-2)x2+2x+1=0有实数根,求m的取值范围
参考答案:
【答案】m≤3且m≠2.
【解析】∵关于x的一元二次方程(m-2)x2+2x+1=0有实数根, ∴m-2≠0且△≥0,即22-4×(m-2)×1≥0,解得m≤3,
∴m的取值范围是 m≤3且m≠2.
【考点精析】认真审题,首先需要了解求根公式(根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠ABC=90°,AC=BD,AC⊥BD,若AB=4, AD=5,则DC的长 ( ).

A. 7 B.
 C.
C.  D. 2
D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=9,AB=CD=15.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE为_________.
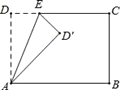
-
科目: 来源: 题型:
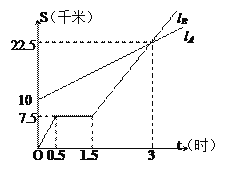
查看答案和解析>>【题目】如图,
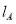 与
与 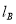 分别表示
分别表示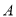 步行与
步行与 骑车同一路上行驶的路程
骑车同一路上行驶的路程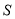 与时间
与时间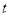 的关系.
的关系.(1)
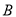 出发时与
出发时与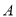 相距多少千米?
相距多少千米?(2)走了一段路后,自行车发生故障,进行修理,所用的时间是多少小时?
(3)
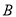 出发后经过多少小时与
出发后经过多少小时与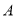 相遇?
相遇? 若
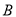 的自行车不发生故障,保持出发时的速度前进,那么经过多少时间与
的自行车不发生故障,保持出发时的速度前进,那么经过多少时间与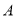 相遇?在图中表示出这个相遇点
相遇?在图中表示出这个相遇点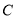 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中, ∠B=∠D=90°,∠DAB与∠DCB 的平分线分别交DC,AB于E,F.求证:AE∥CF.
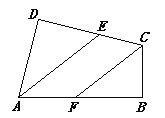
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系的第二象限内有一点P,点P到x轴的距离为2,到y轴的距离为3,则点P的坐标是( )
A.(-3,2)B.(3,-2)C.(2,-3)D.(-2,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.

相关试题

