【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.

参考答案:
【答案】见试题解析
【解析】
试题分析:(1)由OD⊥AC OD为半径,根据垂径定理,即可得![]() ,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可证得BD平分∠ABC;
,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可证得BD平分∠ABC;
(2)首先由OB=OD,易求得∠AOD的度数,又由OD⊥AC于E,可求得∠A的度数,然后由AB是⊙O的直径,根据圆周角定理,可得∠ACB=90°,继而可证得BC=OD.
试题解析:(1)∵OD⊥AC OD为半径,∴![]() ,∴∠CBD=∠ABD,
,∴∠CBD=∠ABD,
∴BD平分∠ABC;
(2)∵OB=OD,∴∠OBD=∠0DB=30°,∴∠AOD=∠OBD+∠ODB=30°+30°=60°,
又∵OD⊥AC于E,∴∠OEA=90°,
∴∠A=180°﹣∠OEA﹣∠AOD=180°﹣90°﹣60°=30°,
又∵AB为⊙O的直径,∴∠ACB=90°,在Rt△ACB中,BC=![]() AB,
AB,
∵OD=![]() AB,
AB,
∴BC=OD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程(m-2)x2+2x+1=0有实数根,求m的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中, ∠B=∠D=90°,∠DAB与∠DCB 的平分线分别交DC,AB于E,F.求证:AE∥CF.
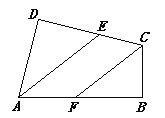
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系的第二象限内有一点P,点P到x轴的距离为2,到y轴的距离为3,则点P的坐标是( )
A.(-3,2)B.(3,-2)C.(2,-3)D.(-2,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD是中线,∠ACB=90°,AC=BC,点E,F分别为AB,AC上的动点(均不与端点重合),且CE⊥BF,垂足为H,BF与CD相交于G.
(1)求证:AE=CG;
(2)当线段AE,CF之间满足什么数量关系时,BF为△ABC的角平分线?请说明理由.
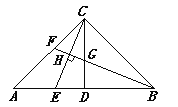
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a既不是正数,也不是负数,b是最小的正整数,c表示下列一组数:
-2,1.5,0,130%, ,860,-3.4中非正数的个数,则a+b+c等于多少?
,860,-3.4中非正数的个数,则a+b+c等于多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】两条直线被第三条直线所截,如果∠1和∠2是同旁内角,且∠1=75°,那么∠2为( )
A.75°
B.105°
C.75°或105°
D.大小不定
相关试题

