搜索
【题目】如图，等腰△ABC中，AB=AC，AD平分∠BAC，点E是线段BC延长线上一点，连接AE，点C在AE的垂直平分线上，若DE=10cm，则AB+BD=cm．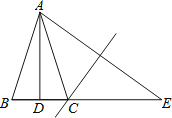
参考答案：
【答案】10
【解析】解：∵点C在AE的垂直平分线上，
∴AC=CE，
∵AB=AC，AD平分∠BAC，
∴BD=CD，
∴AB+BD=AC+CD=CE+CD=DE，
∵DE=10cm，
∴AB+BD=10cm．
所以答案是：10．
【考点精析】利用线段垂直平分线的性质和等腰三角形的性质对题目进行判断即可得到答案，需要熟知垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；等腰三角形的两个底角相等（简称：等边对等角）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某港口位于东西方向的海岸线上．“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里．它们离开港口一个半小时后相距30海里．如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中∠C=90°，放置边长分别为4、6、x的三个正方形，则x的值为（ ）
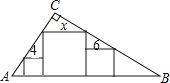
A.24
B.12
C.10
D.8 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
ABCD中，AD=2AB，F是AD的中点，作
，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是（ ）
①
②EF=CF ③
④
A. ①②③ B. ①② C. ②③ ④ D. ①②④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A，C的坐标分别为A（10，0），C（0，4），点D是OA的中点，点P为线段BC上的点．小明同学写出了一个以OD为腰的等腰三角形ODP的顶点P的坐标（3，4），请你写出其余所有符合这个条件的P点坐标 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】(徐州中考)如图，在△ABC中，∠ABC＝90°，∠BAC＝60°，△ACD是等边三角形，E是AC的中点，连接BE并延长交DC于点F，求证：
(1)△ABE≌△CFE；
(2)四边形ABFD是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，E、F分别是边AB、CD上的点，AE=CF，连接EF，BF，EF与对角线AC交于O点，且BE=BF，∠BEF=2∠BAC。
（1）求证：OE=OF；
（2）若BC=
，求AB的长。
相关试题
