【题目】设双曲线![]() 与直线
与直线![]() 交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”,当双曲线
交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”,当双曲线![]() 的眸径为9时,
的眸径为9时,![]() 的值为_____.
的值为_____.

参考答案:
【答案】![]()
【解析】
以 PQ 为边,作矩形 PQQ’P’交双曲线于点 P’、 Q′,联立直线AB及双曲线解析式成方程组,通过解方程组可求出点 A 、 B 的坐标,由 PQ 的长度可得出点 P 的坐标(点 P 在直线 y = - x 上找出点 P的坐标),由图形的对称性结合点 A 、B 和 P 的坐标可得出点 P’ 的坐标,再利用反比例函数图象上点的坐标特征即可得出关于 k 的一元一次方程,解之即可得出结论.
解:以 PQ 为边,作矩形 PQQ’P’交双曲线于点 P 、Q′,如图所示.

联立直线 AB 及双曲线解析式成方程组
解得
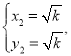
则有点A的坐标为![]() 点B的坐标为
点B的坐标为![]()
又PQ为9,求得点P坐标为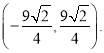
根据图形的对称性可知![]() 得到P’坐标为
得到P’坐标为
将其代入双曲线![]() ,
,
有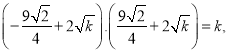
解得![]()
故答案为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人加工同一种玩具,甲加工90个玩具所用的时间与乙加工120个玩具所用的时间相等,已知甲乙两人每天共加工35个玩具,设甲每天加工x个玩具:
(1)乙每天加工 个玩具(用含x的代数式表示);
(2)求甲乙两人每天各加工多少个玩具?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,活动课上,小玥想要利用所学的数学知识测量某个建筑地所在山坡AE的高度,她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1:1的斜坡按速度20米/分步行15分钟到达C处,此时,测得点A的俯角是15°.图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出建筑地所在山坡AE的高度AB.(精确到0.1米,参考数据:
 ≈1.41).
≈1.41).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的两条对角线相交于O,且AC平分∠DAB.
(1)求证:四边形ABCD是菱形;
(2)若AC=8,BD=6,试求点O到AB的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为
 (时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与
(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与 之间的函数关系.
之间的函数关系.
(1)根据图中信息,可知甲乙两地之间的距离为 千米,两车出发 小时相遇;
(2)已知两车相遇时快车比慢车多行驶40千米,求快车从甲地到达乙地所需时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,在梯形
 中,
中, ∥
∥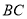 ,
, ,
, ,点
,点 ,
, ,
, 分别在边
分别在边 ,
,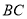 ,
, 上,
上, =
= =
= .
.

(1)求证:四边形
 是平行四边形;
是平行四边形;(2)当
 时,求证:四边形
时,求证:四边形 是矩形;
是矩形;(3)在(2)的条件下,如图2,过点
 作
作 于点
于点 ,当
,当 ,
, ,
, 这三条线段的长度满足怎样的数量关系时,可以判断四边形
这三条线段的长度满足怎样的数量关系时,可以判断四边形 是正方形?并说明理由.
是正方形?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面坐标系
 中,对于点
中,对于点 和点
和点 ,给出如下定义:
,给出如下定义:若
 ,则称点
,则称点 为点
为点 的变限点。例如:点
的变限点。例如:点 的变限点的坐标
的变限点的坐标 ,点
,点 的变限点的坐标
的变限点的坐标 。
。(1)点
 的变限点的坐标是 ;点
的变限点的坐标是 ;点 的变限点的坐标是 .
的变限点的坐标是 .(2)已知直线
 与
与 轴交于点
轴交于点 ,点
,点 在直线
在直线 上,其变限点为
上,其变限点为 ,若
,若 (
( 为坐标原点)的面积等于
为坐标原点)的面积等于 ,求点
,求点 的坐标.
的坐标.(3)已知点
 在函数
在函数 的图象上,其变限点
的图象上,其变限点 的纵坐标
的纵坐标 的取值范围是
的取值范围是 ,求
,求 的取值范围.
的取值范围.
相关试题

