【题目】在平面坐标系![]() 中,对于点
中,对于点![]() 和点
和点![]() ,给出如下定义:
,给出如下定义:
若![]() ,则称点
,则称点![]() 为点
为点![]() 的变限点。例如:点
的变限点。例如:点![]() 的变限点的坐标
的变限点的坐标![]() ,点
,点![]() 的变限点的坐标
的变限点的坐标![]() 。
。
(1)点![]() 的变限点的坐标是 ;点
的变限点的坐标是 ;点![]() 的变限点的坐标是 .
的变限点的坐标是 .
(2)已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在直线
在直线![]() 上,其变限点为
上,其变限点为![]() ,若
,若![]() (
(![]() 为坐标原点)的面积等于
为坐标原点)的面积等于![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)已知点![]() 在函数
在函数![]() 的图象上,其变限点
的图象上,其变限点![]() 的纵坐标
的纵坐标![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() ,
, ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)直接根据变限点的定义![]() ,则称点
,则称点![]() 为点
为点![]() 的变限点,代入点直接得出答案.
的变限点,代入点直接得出答案.
(2) 由直线![]() 与
与![]() 轴交于点
轴交于点![]() 求得A点坐标为
求得A点坐标为![]() ,并代入
,并代入![]() (
(![]() 为坐标原点)的面积等于
为坐标原点)的面积等于![]() ,可知点Q的纵坐标有-3和3两种,分别代入求解即可.
,可知点Q的纵坐标有-3和3两种,分别代入求解即可.
(3)由点Q在函数图像上联立求出b’的取值,并由变限点![]() 的纵坐标
的纵坐标![]() 的取值范围是
的取值范围是![]() ,进行代入最小值b’分别求出x即可.
,进行代入最小值b’分别求出x即可.
解:(1)根据变限点的定义![]() ,将点
,将点![]() 代入可得其变限点的坐标是点Q
代入可得其变限点的坐标是点Q![]() ,将点
,将点![]() 代入可得有
代入可得有![]() 其变限点的坐标是
其变限点的坐标是![]()
(2)由直线![]() 与
与![]() 轴交于点
轴交于点![]() 求得A点坐标为
求得A点坐标为![]() ,点Q在函数
,点Q在函数![]() 的图像上,有
的图像上,有![]() 显然有
显然有![]() 当b’=-3时,-3=-x+2,有x=5,当b’=3时,-3=x-2,有x=-1,所以Q点坐标为
当b’=-3时,-3=-x+2,有x=5,当b’=3时,-3=x-2,有x=-1,所以Q点坐标为![]()
(3)点Q必在函数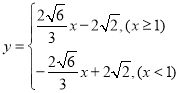 的图像上,则有
的图像上,则有![]() 即当x=1时,b’取得最小值
即当x=1时,b’取得最小值![]() 当
当![]() 时,求得
时,求得![]() 当
当![]()
![]() 若
若![]() 则由图像可知
则由图像可知![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】设双曲线
 与直线
与直线 交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”,当双曲线
交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”,当双曲线 的眸径为9时,
的眸径为9时, 的值为_____.
的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为
 (时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与
(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与 之间的函数关系.
之间的函数关系.
(1)根据图中信息,可知甲乙两地之间的距离为 千米,两车出发 小时相遇;
(2)已知两车相遇时快车比慢车多行驶40千米,求快车从甲地到达乙地所需时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,在梯形
 中,
中, ∥
∥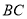 ,
, ,
, ,点
,点 ,
, ,
, 分别在边
分别在边 ,
,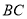 ,
, 上,
上, =
= =
= .
.

(1)求证:四边形
 是平行四边形;
是平行四边形;(2)当
 时,求证:四边形
时,求证:四边形 是矩形;
是矩形;(3)在(2)的条件下,如图2,过点
 作
作 于点
于点 ,当
,当 ,
, ,
, 这三条线段的长度满足怎样的数量关系时,可以判断四边形
这三条线段的长度满足怎样的数量关系时,可以判断四边形 是正方形?并说明理由.
是正方形?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P是双曲线y=
 上的一个动点,连结OP,若将线段OP绕点O逆时针旋转90°得到线段OQ,则经过点Q的双曲线的表达式为__.
上的一个动点,连结OP,若将线段OP绕点O逆时针旋转90°得到线段OQ,则经过点Q的双曲线的表达式为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ACB=90°.请完成以下任务.
(1)尺规作图:①作∠A的平分线,交CB于点D;
②过点D作AB的垂线,垂足为点E.请保留作图痕迹,不写作法,并标明字母.
(2)若AC=3,BC=4,求CD的长.

相关试题

