【题目】如图,AD是△ABC的角平分线,∠B=45°,∠ADC=75°,求∠BAC、∠C的度数.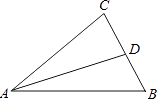
参考答案:
【答案】解:∵∠B=45°,∠ADC=75°,
∴∠BAD=∠ADC﹣∠B=75°﹣45°=30°,
∵AD是△ABC的角平分线,
∴∠BAC=2∠BAD=2×30°=60°,
在△ABC中,∠C=180°﹣∠BAC﹣∠B=180°﹣60°﹣45°=75°.
【解析】首先根据三角形的一个外角等于与它不相邻的两个内角的和可求出∠BAD,再根据角平分线的定义可得∠BAC=2∠BAD,于是可求得∠BAC的度数,最后在△ABC中利用三角形的内角和为180°可求得∠C的度数.
【考点精析】掌握三角形的内角和外角和三角形的外角是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC绕着点B顺时针旋转90°后得到△A2BC2,请在图中画出△A2BC2,并求出线段BC旋转过程中所扫过的面积(结果保留π).
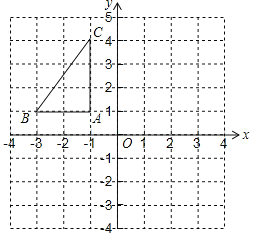
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 (
(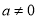 )与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.(1)求此抛物线的解析式;
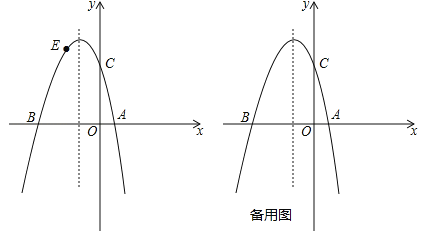
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上.
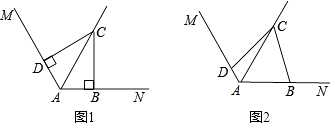
(1)如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;
(2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的三边分别为a、b、c,且(a-b)2+(a2+b2-c2)2=0,则三角形的形状为————————————————。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,BE的垂直平分线MN恰好过点C.则矩形的一边AB的长度为( )
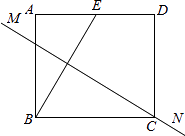
A.1
B.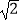
C.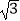
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )
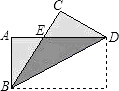
A.△EBD是等腰三角形,EB=ED
B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA和△EDC一定是全等三角形
相关试题

