【题目】如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,BE的垂直平分线MN恰好过点C.则矩形的一边AB的长度为( ) 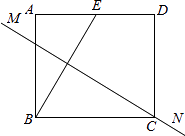
A.1
B.![]()
C.![]()
D.2
参考答案:
【答案】C
【解析】解:如图,连接EC. 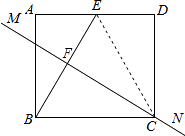
∵FC垂直平分BE,
∴BC=EC(线段垂直平分线的性质)
又∵点E是AD的中点,AE=1,AD=BC,
故EC=2,
利用勾股定理可得AB=CD= ![]() =
= ![]() .
.
故选:C.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上.
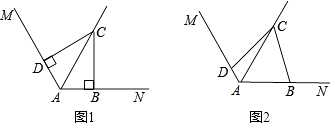
(1)如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;
(2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由. -
科目: 来源: 题型:
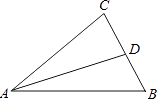
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,∠B=45°,∠ADC=75°,求∠BAC、∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的三边分别为a、b、c,且(a-b)2+(a2+b2-c2)2=0,则三角形的形状为————————————————。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )
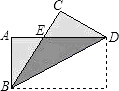
A.△EBD是等腰三角形,EB=ED
B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA和△EDC一定是全等三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
(1)求证:PQ∥AB;
(2)若点D在∠BAC的平分线上,求CP的长;
(3)若△PDE与△ABC重叠部分图形的周长为T,且12≤T≤16,求x的取值范围.
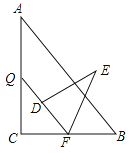
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )

A.12
B.24
C.12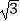
D.16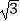
相关试题

