【题目】解方程:
(1)-6x+2=2x-14;
(2)4y-3(20-y)=6y+7(y-1);
(3)![]() =1.
=1.
参考答案:
【答案】(1)x=2;(2)y=-![]() ;(3)x=0.
;(3)x=0.
【解析】
(1)移项、合并同类项、化系数为1即可求出x的值;
(2)先去括号,再移项、合并同类项、化系数为1即可求出y的值;
(3)去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.括号前若有负号,去括号时都要变号.
(1)移项,合并同类项得:-8x=-16,
把系数化为1,得x=2;
(2)去括号得:4y-60+3y=6y-7+7y,
移项,合并同类项得:-6y=53,
把系数化为1,得y= ![]() ;
;
(3)去分母得:3(x+2)-2(2x-3)=12,
去括号得:3x+6-4x+6=12,
移项、合并同类项得:- x=0,
把系数化为1得:x=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在日历上,我们可以发现其中某些数满足一定的规律,如图是2017年12月份的日历.如图所选择的两组四个数,分别将每组数中相对的两数相乘,再相减,例如:7×9﹣1×15= ,18×20﹣12×26= ,不难发现,结果都是 .

(1)请将上面三个空补充完整;
(2)我们发现选择其他类似的部分规律也相同,请你利用整式的运算对以上的规律加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC是弦.
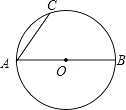
(1)请你按下面步骤画图(画图或作辅助线时先使用铅笔画出,确定后必须使用黑色字迹的签字笔描黑); 第一步,过点A作∠BAC的角平分线,交⊙O于点D;
第二步,过点D作AC的垂线,交AC的延长线于点E.
第三步,连接BD.
(2)求证:AD2=AEAB;
(3)连接EO,交AD于点F,若5AC=3AB,求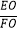 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在商场购买甲、乙两种不同足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元?
(2)为响应“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%,如果此次购买甲、乙两种足球的总费用不超过2900元,那么这所学校最多可购买多少个乙种足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大酒店有108个相同规格的房间需要装饰.一天,3名师傅去装饰8个房间,结果其中有40平方米未来得及装饰;同样一天5名徒弟去恰好装饰完9个房间.已知每名师傅比徒弟一天多装饰30平方米.
(1)求每个房间需要装饰的面积;
(2)每名师傅每天装饰多少平方米?每名徒弟呢?
(3)若由1名师傅带2名徒弟去装饰这108个房间,需要几天才能完成?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=2,AC=BC=
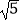 .
.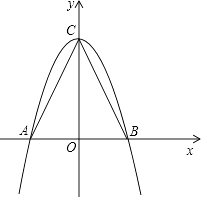
(1)以AB所在的直线为x轴,AB的垂直平分线为y轴,建立直角坐标系如图,请你分别写出A、B、C三点的坐标;
(2)求过A、B、C三点且以C为顶点的抛物线的解析式;
(3)若D为抛物线上的一动点,当D点坐标为何值时,S△ABD= S△ABC;
S△ABC;
(4)如果将(2)中的抛物线向右平移,且与x轴交于点A′B′,与y轴交于点C′,当平移多少个单位时,点C′同时在以A′B′为直径的圆上(解答过程如果有需要时,请参看阅读材料).
附:阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法,对于一些特殊方程可以通过换元法转化为一元二次方程求解.如解方程:y4﹣4y2+3=0.
解:令y2=x(x≥0),则原方程变为x2﹣4x+3=0,解得x1=1,x2=3.
当x1=1时,即y2=1,∴y1=1,y2=﹣1.
当x2=3,即y2=3,∴y3=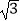 ,y4=﹣
,y4=﹣ 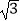 .
.
所以,原方程的解是y1=1,y2=﹣1,y3=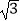 ,y4=﹣
,y4=﹣ 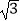 .
.
再如x2﹣2=4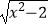 ,可设y=
,可设y= 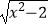 ,用同样的方法也可求解.
,用同样的方法也可求解. -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数按要求分类.
﹣2,5,
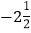 ,0,﹣3.4,﹣21,π,
,0,﹣3.4,﹣21,π, ,3.7,15%;
,3.7,15%;正数集合:{_____…},
负整数集合:{_____…},
分数集合:{_____…}
非正数集合:{_____…}
相关试题

