搜索
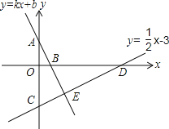
【题目】如图，点A、B的坐标分别为（0，2），（1，0），直线y=
﹣3与坐标轴交于C、D两点．
（1）求直线AB：y=kx+b与CD交点E的坐标；
（2）直接写出不等式kx+b＞﹣3的解集；
（3）求四边形OBEC的面积；
参考答案：
【答案】（1）（2，﹣2）；（2）x＜2；（3）
.
【解析】
（1）利用待定系数法求出直线AB的解析式，利用二元一次方程组求出点E的坐标；
（2）根据函数图象写出不等式kx+b>
x-3的解集；
（3）根据坐标轴上点的特征求出C、D两点的坐标，根据三角形的面积公式计算即可.
解：（1）由题意得
，
解得
，
故直线AB的解析式是y=﹣2x+2，
则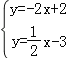
解得
，
故点E的坐标是（2，﹣2）；
（2）由图象可知，x＜2时，y=kx+b的图象在y=
﹣3的图象的上方，
故不等式kx+b＞
x﹣3的解集是x＜2；
（3）y=﹣3，
当x=0时，y=﹣3，当y=0时，x=6，
则点C的坐标是（0，﹣3），点D的坐标是（6，0）
四边形OBEC的面积=△DOC的面积-△BOE的面积=
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在△ABC中，∠CAB=70°，将△ABC绕点A按逆时针方向旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′的度数为 ．
-
科目： 来源： 题型：
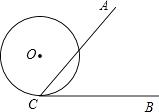
查看答案和解析>>【题目】如图，∠ACB=60°，半径为1cm的⊙O切BC于点C，若将⊙O在CB上向右滚动，则当滚动到⊙O与CA也相切时，圆心O移动的水平距离是cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠B=60°，∠C=20°，AD为△ABC的高，AE为角平分线．求∠EAD的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A（2，3），B（1，1），C（4，1），M（6，3）．
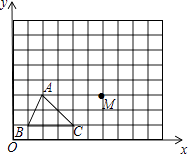
（1）将△ABC平原得到△A1B1C1 ， 其中点A，B，C的对应点分别是A1 ， B1 ， C1 ， 且点A1的坐标是（3，6），在图中画出△A1B1C1 ．
（2）将（1）中的△A1B1C1绕点M顺时针旋转90°，画出旋转后的△A2B2C2（其中点A2 ， B2 ， C2的对应点分别是A1 ， B1 ， C1），并写出点A2 ， B2 ， C2的坐标．
（3）（2）中的△A2B2C2能通过旋转△ABC得到吗？若能，请写出旋转的方案． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点D，过点B作BE垂直于PD，交PD的延长线于点C，连接AD并延长，交BE于点E． 求证：AB=BE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某个体户购进一批时令水果，20天销售完毕，他将本次销售情况进行了跟踪记录，根据所记录的数据绘制如下的函数图象，其中日销售量y(千克)与销售时间x(天)之间的函数关系如图(1)所示，销售单价p(元/千克)与销售时间x(天)之间的函数关系如图(2)所示。(销售额=销售单价×销售量)
(1)直接写出y与x之间的函数解析式；
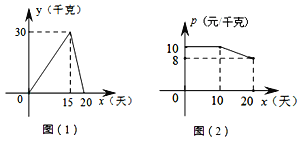
(2)分别求第10天和第15天的销售额；
(3)若日销售量不低于24千克的时间段为“最佳销售期”，则此次销售过程中，“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
相关试题
