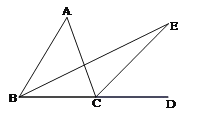
【题目】如图所示,∠ACD是△ABC的外角, BE平分∠ABC, CE平分∠ACD,且BE、CE交于点E。试找出∠A与∠E的关系。
参考答案:
【答案】∠A=2∠E,理由见解析.
【解析】试题分析:由三角形的一个外角等于与它不相邻的两个内角的和,得∠ACD=∠A+∠ABC,∠ECD=∠E+∠EBC;由角平分线的定义,得∠ECD=![]() (∠A+∠ABC),∠EBC=
(∠A+∠ABC),∠EBC=![]() ∠ABC,利用等量代换,即可求得∠A与∠E的关系.
∠ABC,利用等量代换,即可求得∠A与∠E的关系.
试题解析:∵∠ACD=∠A+∠ABC,
∴∠ECD=![]() (∠A+∠ABC).
(∠A+∠ABC).
又∵∠ECD=∠E+∠EBC,
∴∠E+∠EBC=![]() (∠A+∠ABC).
(∠A+∠ABC).
∵BE平分∠ABC,
∴∠EBC=![]() ∠ABC,
∠ABC,
∴![]() ∠ABC+∠E=
∠ABC+∠E=![]() (∠A+∠ABC),
(∠A+∠ABC),
∴∠E=![]() ∠A,
∠A,
即∠A=2∠E.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是( )

A. 25° B. 30° C. 35° D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;
(2)求∠DFC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A1(1,1),A2(2,4),A3(3,9),A4(4,16),…,用你发现的规律确定点A9的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个四边形四个内角度数之比是2∶2∶3∶5,那么这四个内角中( ).
A. 只有一个直角 B. 只有一个锐角 C. 有两个直角 D. 有两个钝角
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3 , …组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒
 个单位长度,则第2017秒时,点P的坐标是( )
个单位长度,则第2017秒时,点P的坐标是( )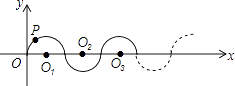
A.(2016,0)
B.(2017,1)
C.(2017,﹣1)
D.(2018,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于实数a,符号[a]表示不大于a的最大整数,例如:[4.7]=4,[﹣π]=﹣4,[3]=3,如果[
 +1]=﹣5,则x的取值范围为 .
+1]=﹣5,则x的取值范围为 .
相关试题

