【题目】某文具店出售A,B两种笔记本,其中购买2本A型笔记本和3本B型笔记本花费42元,购买3本A型笔记本和2本B型笔记本花费38元.
(1)A型笔记本和B型笔记本的单价为多少元?
(2)若一次购买B型笔记本超过20本时,超过20本部分的B型记笔记价格打8折,分别写出两种笔记本的付款金额y(元)关于购买量x(本)的函数解析式;
(3)某校准备在一次学习竞赛后购买这90本两种笔记本用于奖励,其中A型笔记本数量不超过B型笔记本的一半,两种笔记本各买多少时,总费用最少,最少费用是多少元?
参考答案:
【答案】(1) 6元、8元 (2)A型: y=6x;B型: y=20×8+(x﹣20)×0.8×8=6.4x+32 (3)596元
【解析】
(1)设购买一本A型笔记本和一本B型笔记本分别需要x元、y元,根据“购买2本A型笔记本和3本B型笔记本花费42元,购买3本A型笔记本和2本B型笔记本花费38元”,列出方程组,解方程组即可求得A型笔记本和B型笔记本的单价;(2)根据题意写出两种笔记本的付款金额y(元)关于购买量x(本)的函数解析式即可;(3)设A型笔记本数量为a,则B型笔记本的数为90-a,根据A型笔记本数量不超过B型笔记本的一半列出不等式,解不等式求得x的取值范围,结合取值范围及两种笔记本的单价即可求得最少费用.
(1)设购买一本A型笔记本和一本B型笔记本分别需要x元、y元,
![]() ,得
,得![]() ,
,
答:购买一本A型笔记本和一本B型笔记本分别需要6元、8元;
(2)由题意可得:A型笔记本的付款金额y(元)关于购买量x(本)的函数解析式为:y=6x;
B型笔记本的付款金额y(元)关于购买量x(本)的函数解析式为:y=20×8+(x﹣20)×0.8×8=6.4x+32(x>20);
(3)设A型笔记本数量为a,根据题意可得:
a≤![]() ,
,
解得:a≤30,
当a=30,90﹣a=60时,总费用最少,最少费用是6×30+6.4××60+32=596元,
即A型笔记本数量为30本,B型笔记本数量为60本时,总费用最少,最少费用是596元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.

(1)求证:AE平分∠BAD.
(2)求证:AD=AB+CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE.
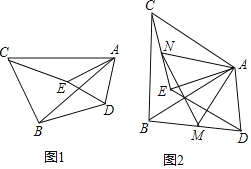
(1)求证:BD=CE;
(2)若点M,N分别是BD,CE的中点,如图2,连接AM,AN,MN,若AC=6,AE=4,∠EAC=60°,求AN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)某数学兴趣小组想测量商丘电视台电视塔的高度,如图,该小组在商丘电视塔BC前一座楼房楼顶A处所观测到电视塔最高点B的仰角为65°,电视塔最低点C的仰角为30°,楼顶A与电视塔的水平距离AD为90米,求商丘电视塔BC的高度.(结果精确到1米,参考数据
 ≈1.41,
≈1.41, ≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班“数学兴趣小组”对函数y=
 +x的图象与性质进行了探究,探究过程如下,请补充完整.
+x的图象与性质进行了探究,探究过程如下,请补充完整.(1)函数y=
 +x的自变量x的取值范围是 ;
+x的自变量x的取值范围是 ;(2)下表是y与x的几组对应值.
x
…
﹣3
﹣2
﹣1
0




2
3
4
5
…
y
…
﹣

﹣

﹣

﹣1
﹣

﹣



3

m

…
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可): .
(5)小明发现,①该函数的图象关于点( , )成中心对称;
②该函数的图象与一条垂直于x轴的直线无交点,则这条直线为 ;
③直线y=m与该函数的图象无交点,则m的取值范围为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB是锐角,点D在射线BC上运动,连接AD,将线段AD绕点A逆时针旋转90°,得到AE,连接EC.
(1)操作发现:若AB=AC,∠BAC=90°,当D在线段BC上时(不与点B重合),如图①所示,请你直接写出线段CE和BD的位置关系和数量关系是 , ;
(2)猜想论证:
在(1)的条件下,当D在线段BC的延长线上时,如图②所示,请你判断(1)中结论是否成立,并证明你的判断.
(3)拓展延伸:
如图③,若AB≠AC,∠BAC≠90°,点D在线段BC上运动,试探究:当锐角∠ACB等于 度时,线段CE和BD之间的位置关系仍成立(点C、E重合除外)?此时若作DF⊥AD交线段CE于点F,且当AC=3
 时,请直接写出线段CF的长的最大值是
时,请直接写出线段CF的长的最大值是 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,A(a,0),B(0,b),D(0,c),其中a,b,c满足2a2+b2+c2-2ab-8a-2c+17=0,过坐标O作直线BC交线段OA于点C.
(1)如图1,当∠ODA=∠OCB时,求点C的坐标;
(2)如图2,在(1)条件下,过O作OE⊥BC交AB于点E,过E作EF⊥AD交OA于点N,交BC延长线于F,求证:BF=OE+EF;

相关试题

