【题目】已知在平面直角坐标系中,A(a,0),B(0,b),D(0,c),其中a,b,c满足2a2+b2+c2-2ab-8a-2c+17=0,过坐标O作直线BC交线段OA于点C.
(1)如图1,当∠ODA=∠OCB时,求点C的坐标;

(2)如图2,在(1)条件下,过O作OE⊥BC交AB于点E,过E作EF⊥AD交OA于点N,交BC延长线于F,求证:BF=OE+EF;

参考答案:
【答案】(1)C(1,0);(2)见解析;
【解析】
(1)利用非负数的性质求出a,b,c的值,再证明△AOD≌△BOC(ASA),推出OC=OD=1解决问题;
(2)如图2中,设AD交BC于点Q,连接OQ,QE.想办法证明BQ=OE,FQ=EF即可解决问题;
(1)如图1中,
∵2a2+b2+c2-2ab-8a-2c+17=0,
∴(a-4)2+(a-b)2+(c-1)2=0,
∵(a-4)2≥0,(a-b)2≥0,(c-1)2≥0,
∴a=b=4,c=1,
∴A(4,0),B(0,4),D(0,1).
∴OB=OA,
∵∠ODA=∠OCB,∠AOD=∠BOC=90°,
∴△AOD≌△BOC(ASA),
∴OC=OD=1,
∴C(1,0).
(2)如图2中,设AD交BC于点Q,连接OQ,QE.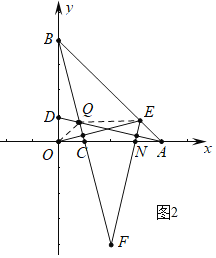
∵△AOD≌△BOC,
∴∠DAO=∠CBO,OD=OC,
∵OB=OA,
∴BD=AC,
∵∠AQB=∠CQA,
∴△DQB≌△CQA(AAS),
∴BQ=AQ,
∵OQ=OQ,OB=OA,BQ=AQ,
∴△OQB≌△OQA(SSS),
∴∠BOQ=∠AOQ=45°,
∴∠BOQ=∠OAE,
∵BF⊥OE,
∴∠OBC+∠BOE=90°,∠BOE+∠AOE=90°,
∴∠OBQ=∠AOE,∵OB=OA,
∴△OBQ≌△AOE(ASA),
∴BQ=OE,OQ=AE,
∵EQ=EQ,AQ=OE,OQ=AE,
∴△OEQ≌△AQE(SSS),
∴∠OEQ=∠AQE,
∵EF⊥AD,OE⊥BC,
∴∠F+∠FEO=90°,∠F+∠FQA=90°,
∴∠FEO=∠FQA,
∴∠FEQ=∠FQE,
∴EF=FQ,
∴BF=BQ+FQ=OE+EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店出售A,B两种笔记本,其中购买2本A型笔记本和3本B型笔记本花费42元,购买3本A型笔记本和2本B型笔记本花费38元.
(1)A型笔记本和B型笔记本的单价为多少元?
(2)若一次购买B型笔记本超过20本时,超过20本部分的B型记笔记价格打8折,分别写出两种笔记本的付款金额y(元)关于购买量x(本)的函数解析式;
(3)某校准备在一次学习竞赛后购买这90本两种笔记本用于奖励,其中A型笔记本数量不超过B型笔记本的一半,两种笔记本各买多少时,总费用最少,最少费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班“数学兴趣小组”对函数y=
 +x的图象与性质进行了探究,探究过程如下,请补充完整.
+x的图象与性质进行了探究,探究过程如下,请补充完整.(1)函数y=
 +x的自变量x的取值范围是 ;
+x的自变量x的取值范围是 ;(2)下表是y与x的几组对应值.
x
…
﹣3
﹣2
﹣1
0




2
3
4
5
…
y
…
﹣

﹣

﹣

﹣1
﹣

﹣



3

m

…
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可): .
(5)小明发现,①该函数的图象关于点( , )成中心对称;
②该函数的图象与一条垂直于x轴的直线无交点,则这条直线为 ;
③直线y=m与该函数的图象无交点,则m的取值范围为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB是锐角,点D在射线BC上运动,连接AD,将线段AD绕点A逆时针旋转90°,得到AE,连接EC.
(1)操作发现:若AB=AC,∠BAC=90°,当D在线段BC上时(不与点B重合),如图①所示,请你直接写出线段CE和BD的位置关系和数量关系是 , ;
(2)猜想论证:
在(1)的条件下,当D在线段BC的延长线上时,如图②所示,请你判断(1)中结论是否成立,并证明你的判断.
(3)拓展延伸:
如图③,若AB≠AC,∠BAC≠90°,点D在线段BC上运动,试探究:当锐角∠ACB等于 度时,线段CE和BD之间的位置关系仍成立(点C、E重合除外)?此时若作DF⊥AD交线段CE于点F,且当AC=3
 时,请直接写出线段CF的长的最大值是
时,请直接写出线段CF的长的最大值是 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,AD=AE,,若要得到△ABD≌△ACE,必须添加一个条件,则下列所添条件不恰当的是 ( ).

A. BD=CEB. ∠ABD=∠ACEC. ∠BAD=∠CAED. ∠BAC=∠DAE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,△ABC的三个顶点的坐标分别为A(1,5),B(1,-2),C(4,0).
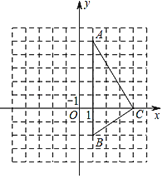
(1)请在图中画出△ABC关于y轴对称的△
 .
.(2)求△ABC的面积.
(3)在y轴上画出点P,使PA+PC的值最小,保留作图痕迹.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上张老师将课本44页第4题进行了改编,图形不变.请你完成下问题.


(1)如图1,∠ACB=∠ADB,BC=BD,求证:△ABC≌△ABD.
(2)如图2,∠CAB=∠DAB,BC=BD,求证:△ABC≌△ABD.
相关试题

