【题目】如图1,△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE.
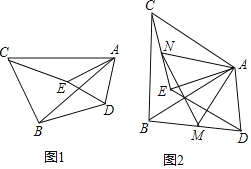
(1)求证:BD=CE;
(2)若点M,N分别是BD,CE的中点,如图2,连接AM,AN,MN,若AC=6,AE=4,∠EAC=60°,求AN的长.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由∠BAC=∠DAE知∠EAC=∠DAB,根据AB=AC、AD=AE即可证△CAE≌△BAD,从而得证;
(2)取AC的中点F,连接FN,过点N作NG⊥AC,据此可得NF∥AE、NF=![]() AE=2,继而由∠GFN=∠EAC=60°得FG=
AE=2,继而由∠GFN=∠EAC=60°得FG=![]() FN=1、AG=4、NG=
FN=1、AG=4、NG=![]() ,利用勾股定理可得答案.
,利用勾股定理可得答案.
(1)∵∠BAC=∠DAE,
∴∠BAC-∠BAE=∠DAE-∠BAE,
∴∠EAC=∠DAB,
∵AB=AC、AD=AE,
∴△CAE≌△BAD,
∴BD=CE;
(2)取AC的中点F,连接FN,过点N作NG⊥AC于点G,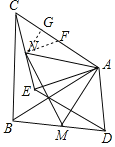
∵N是CE的中点,
∴NF∥AE,NF=![]() AE=2,
AE=2,
∴∠GFN=∠EAC=60°,
∴∠FNG=30°,
∴FG=![]() FN=1,
FN=1,
∴AG=1+3=4,NG=![]() ,
,
在Rt△ANG中,由勾股定理可得AN=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学生的体能状况,某学校从七年级学生中随机抽取部分学生的体能测试结果进行分析,并根据收集的数据绘制了两幅不完整的统计图,请根据这两幅统计图中的信息回答下列问题:(测试结果分“优秀”、“良好”、“及格”、“不及格”四个等级)
(1)本次抽样调查共抽取多少名学生?
(2)补全条形统计图.
(3)在扇形统计图中,求测试结果为“良好”等级所对应圆心角的度数.
(4)若该学校七年级共有600名学生,请你估计该学校七年级学生中测试结果为“不及格”等级的学生有多少名?

-
科目: 来源: 题型:
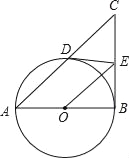
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D作⊙O的切线交BC于点E,连接OE
(1)证明OE∥AD;
(2)①当∠BAC= °时,四边形ODEB是正方形.
②当∠BAC= °时,AD=3DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.

(1)求证:AE平分∠BAD.
(2)求证:AD=AB+CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)某数学兴趣小组想测量商丘电视台电视塔的高度,如图,该小组在商丘电视塔BC前一座楼房楼顶A处所观测到电视塔最高点B的仰角为65°,电视塔最低点C的仰角为30°,楼顶A与电视塔的水平距离AD为90米,求商丘电视塔BC的高度.(结果精确到1米,参考数据
 ≈1.41,
≈1.41, ≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店出售A,B两种笔记本,其中购买2本A型笔记本和3本B型笔记本花费42元,购买3本A型笔记本和2本B型笔记本花费38元.
(1)A型笔记本和B型笔记本的单价为多少元?
(2)若一次购买B型笔记本超过20本时,超过20本部分的B型记笔记价格打8折,分别写出两种笔记本的付款金额y(元)关于购买量x(本)的函数解析式;
(3)某校准备在一次学习竞赛后购买这90本两种笔记本用于奖励,其中A型笔记本数量不超过B型笔记本的一半,两种笔记本各买多少时,总费用最少,最少费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班“数学兴趣小组”对函数y=
 +x的图象与性质进行了探究,探究过程如下,请补充完整.
+x的图象与性质进行了探究,探究过程如下,请补充完整.(1)函数y=
 +x的自变量x的取值范围是 ;
+x的自变量x的取值范围是 ;(2)下表是y与x的几组对应值.
x
…
﹣3
﹣2
﹣1
0




2
3
4
5
…
y
…
﹣

﹣

﹣

﹣1
﹣

﹣



3

m

…
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可): .
(5)小明发现,①该函数的图象关于点( , )成中心对称;
②该函数的图象与一条垂直于x轴的直线无交点,则这条直线为 ;
③直线y=m与该函数的图象无交点,则m的取值范围为 .

相关试题

