【题目】如图,已知等腰△ABC顶角∠A=36°.
(1)尺规作图:在AC上作一点D,使AD=BD;(保留作图痕迹,不必写作法和证明)
(2)求证:△BCD是等腰三角形.

参考答案:
【答案】(1)见解析;(2)△BCD是等腰三角形
【解析】
(1)根据垂直平分线的尺规作图方法,作AB的垂直平分线交AC于点D,点D即为所求.
(2)已知等腰△ABC顶角∠A=36°,![]() ,再证明∠BDC=72°,即可证明△BCD是等腰三角形.
,再证明∠BDC=72°,即可证明△BCD是等腰三角形.
(1)如图1,作AB的垂直平分线,分别以点A、B为圆心,以大于![]() 为半径在AB上方画弧,在AB上方两圆弧交点为点M,分别以点A、B为圆心以大于
为半径在AB上方画弧,在AB上方两圆弧交点为点M,分别以点A、B为圆心以大于![]() 为半径在AB下方画弧,在AB下方两圆弧交点为点N.过点M、N作直线MN,交AC于点D,点D即为所求.
为半径在AB下方画弧,在AB下方两圆弧交点为点N.过点M、N作直线MN,交AC于点D,点D即为所求.
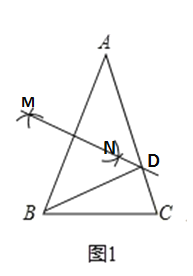
(2)∵在等腰△ABC顶角∠A=36°
∴![]()
∵AD=BD
∴∠ABD=∠A=36°
则∠DBC=36°
在△BCD中∠ACB=72°
∠DBC=36°
∠BDC=72°=∠ACB
∴△BCD是等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读以下材料,并按要求完成相应的任务.
在初中数学课本中重点介绍了提公因式法和运用公式法两种因式
分解的方法,其中运用公式法即运用平方差公式:
 和完全平方公式:
和完全平方公式: 进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接能运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式
进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接能运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式
 变形为
变形为 的形式,我们把这样的变形方法叫做多项式
的形式,我们把这样的变形方法叫做多项式 的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.例如:




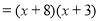 .
.根据以上材料,完成相应的任务:
(1)利用“多项式的配方法”将
 化成
化成 的形式为_______;
的形式为_______;(2)请你利用上述方法因式分解:
①
 ; ②
; ② .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
如图1,
 和
和 都是等腰直角三角形,其中
都是等腰直角三角形,其中 ,点
,点 在线段
在线段 上.
上.
操作发现:如图2,保持点
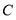 不动,
不动, 绕点
绕点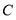 按顺时针旋转角度
按顺时针旋转角度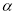 (
( ),连接
),连接 与
与 .
.
(1)猜想线段
 ,
, 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;拓展探究:如图3,
 绕点
绕点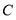 继续按顺时针旋转,当点
继续按顺时针旋转,当点 ,
, ,
, 在同一直线上时,过点
在同一直线上时,过点 作
作 ,垂足为
,垂足为 .
.
(2)求
 的度数;
的度数;(3)直接写出线段
 ,
, ,
, 之间的的数量关系.
之间的的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:
(1)AD=BD;
(2)DF是⊙O的切线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:

(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.


请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
-
科目: 来源: 题型:
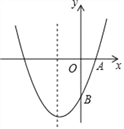
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且经A(1,0)、
B(0,﹣3)两点.(1)求抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上,是否存在点M,使它到点A的距离与到点B的距离之和最小,如果存在求出点M的坐标,如果不存在请说明理由.
相关试题

