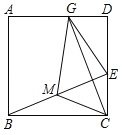
【题目】如图,在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为____.
参考答案:
【答案】9.
【解析】
证明△BCE≌△CDG(ASA),可得BE=CG,根据直角三角形斜边中线的性质可得CG=BE=2CM=6,最后根据面积和可得四边形GMCE的面积.
解:令BE、CG交于点O,

∵四边形ABCD是正方形,
∴BC=CD,∠D=∠BCE=90°.
∵CG⊥BE,
∴∠COE=∠CEO+∠ECO=∠CEO+∠CBE=90°,
∴∠ECO=∠CBE,
在△BCE和△CDG中,
∵ ,
,
∴△BCE≌△CDG(ASA),
∴BE=CG.
∵CM=3,∠BCE=90°,且M是BE的中点,
∴CG=BE=2CM=6,
∴四边形GMCE的面积=S△EMG+S△CME=![]() .
.
故答案为:9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
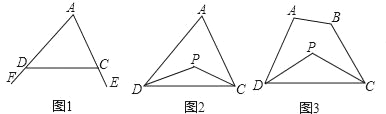
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:

(1)请将下表补充完整:

(2)请从下列三个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,两个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O.
(1)在图1中,你发现线段AC,BD的数量关系是 ,直线AC,BD相交成 度角.
(2)将图1中的△OAB绕点O顺时针旋转90°角,这时(1)中的两个结论是否成立?请做出判断并说明理由.
(3)将图1中的△OAB绕点O顺时针旋转一个锐角,得到图3,这时(1)中的两个结论是否成立?请作出判断并说明理由.

-
科目: 来源: 题型:
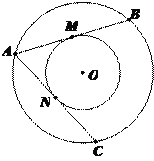
查看答案和解析>>【题目】如图,大圆的弦AB、AC分别切小圆于点M、N.
(1)求证:AB=AC;
(2)若AB=8,求圆环的面积.
-
科目: 来源: 题型:
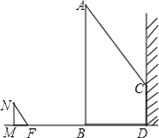
查看答案和解析>>【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
-
科目: 来源: 题型:
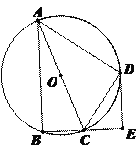
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,
 ,AC为直径, DE⊥BC,垂足为E.
,AC为直径, DE⊥BC,垂足为E.(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
相关试题

