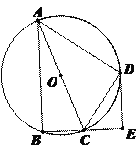
【题目】如图,四边形ABCD是⊙O的内接四边形, ![]() ,AC为直径, DE⊥BC,垂足为E.
,AC为直径, DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
参考答案:
【答案】(1)证明见解析;(2)CD=3![]()
【解析】试题分析:(1)根据圆周角定理,由弧AD=弧BD可得∠BAD=∠ACD,再根据圆内接四边形的性质得∠DCE=∠BAD,所以∠ACD=∠DCE;
(2)先证明△DCE∽△ACD,再根据相似三角形的性质列比例式求解.
证明:(1)∵四边形ABCD是⊙O内接四边形,∴∠BAD+∠BCD=180°,
∵∠BCD+∠DCE=180°,∴∠DCE=∠BAD,
∵![]() =
=![]() ,∴∠BAD=∠ACD,
,∴∠BAD=∠ACD,
∴∠DCE=∠ACD,
∴CD平分∠ACE.
(2)∵AC为直径,∴∠ADC=90°,
∵DE⊥BC,∴∠DEC=90°,∴∠DEC=∠ADC…
∵∠DCE=∠ACD,∴△DCE∽△ACD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CD=3![]()
-
科目: 来源: 题型:
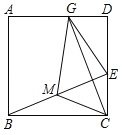
查看答案和解析>>【题目】如图,在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为____.
-
科目: 来源: 题型:
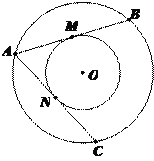
查看答案和解析>>【题目】如图,大圆的弦AB、AC分别切小圆于点M、N.
(1)求证:AB=AC;
(2)若AB=8,求圆环的面积.
-
科目: 来源: 题型:
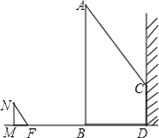
查看答案和解析>>【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,∠E=∠F=90°,∠B=∠C,AC=AB,给出下列结论:① ∠1=∠2;② BE=CF;③ △ACN≌△ABM;④ CD=DN,其中正确的结论有( )个

A.1B.2C.3D.4
-
科目: 来源: 题型:
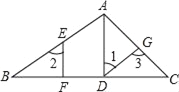
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F.
(1)AD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠BAC的度数.
相关试题

