【题目】如图所示,甲、乙两块边长为a米(a>1)的正方形田地,甲地修了两条互相垂直的宽为1米的通道,乙地正中间修了边长为1米的蓄水池,甲乙两田地的剩余地方全部种植小麦,一年后收获小麦m千克.(m>0)

(1)甲地的小麦种植面积为 平方米,乙地的小麦种植面积为 平方米;
(2)甲乙两地小麦种植面积较小的是 地;
(3)若高的单位面积产量是低的单位面积产量的![]() 倍,求a的值.
倍,求a的值.
参考答案:
【答案】(1)(a﹣1)2,(a2﹣1);(2)甲;(3)a的值为99.
【解析】
(1)根据矩形面积计算公式,列出关于a的代数式.(2)根据a的取值范围,判断两个代数式的大小.(3)根据等量关系列出方程,化简求值.
解:(1)甲地的小麦种植面积为:(a﹣1)2(平方米);
乙地的小麦种植面积=a2﹣12=a2﹣1(平方米).
故答案为:(a﹣1)2,(a2﹣1);
(2)∵(a﹣1)2﹣(a2﹣1)=a2﹣2a+1﹣a2+1=﹣2a+2=﹣2(a﹣1),
又a>1,∴a﹣1>0,
∴﹣2(a﹣1)<0,
∴(a﹣1)2<a2﹣1,
∴甲乙两地小麦种植面积较小的是甲地.
故答案为甲;
(3)∵高的单位面积产量是低的单位面积产量的![]() 倍,
倍,
∴![]() =
=![]() ×
×![]() ,
,
整理,得a2﹣100a+99=0,
解得a1=1(舍去),a2=99,
经检验,a=99是原方程的根.
故所求a的值为99.
-
科目: 来源: 题型:
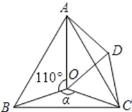
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当∠BOC为多少度时,△AOD是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的解题过程:
计算:(-15)÷
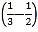 ×6.
×6.解:原式=(-15)÷
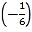 ×6(第一步)
×6(第一步)=(-15)÷(-1)(第二步)
=-15.(第三步)
回答:(1)上面解题过程中有两处错误,第一处是第________步,错误的原因是________________;第二处是第________,错误的原因是________________.
(2)把正确的解题过程写出来.
-
科目: 来源: 题型:
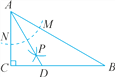
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧,分别交AB,AC于点M和N,再分别以点M,N为圆心,大于
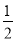 MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的个数是( )
MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的个数是( )①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC∶S△ABC=1∶3.
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】沾益区兴隆水果店计划用1000元购进甲、乙两种新出产的水果140千克,这两种水果的进价、售价如下表所示:
进价(元/千克)
售价(元/千克)
甲
5
8
乙
9
13
(1)这两种水果各购进多少千克?
(2)该水果店全部销售完这批水果时获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】邮递员骑车从邮局出发,先向西骑行 2 km 到达 A 村,继续向西骑行 3 km 到达 B 村, 然后向东骑行 9 km 到达 C 村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用 1 cm 表示 1 km 画数轴,并在该数轴上表示 A,B,C 三个村庄的位置;
(2)C 村离 A 村有多远?
(3)邮递员一共骑行了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,CA=CB,∠ACB=120°,点E、F在AB上,且∠ECF=60°.
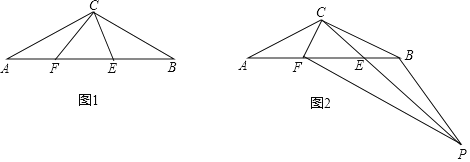
(1)①在图1中画出;点A关于直线CF的对称点G;②若EF=AF,求证:BE=EF;
(2)如图2,∠ABP=120°,射线BP交CE的延长线于点P,求证:PB+AF=PF.
相关试题

