【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AF=2,EB=1,求AB的长.

参考答案:
【答案】(1)证明见解析;(2)4
【解析】(1)由AD为角平分线,利用角平分线定理得到DE=DC,再由BD=DF,利用HL得到三角形FCD与三角形BDF全等,利用全等三角形对应边相等即可得证;
(2)利用AAS得到三角形ACD与三角形AED全等,利用全等三角形对应边相等得到AC=AE,由AB=AE+EB,等量代换即可得证.
(1)证明:∵ AD是∠BAC的平分线,∠C=90°,DE⊥AB
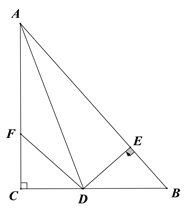
∴ DC=DE
∵ BD=DF
∴Rt△DCF≌Rt△DEB
∴CF=EB
(2)解:由(1)知CF=EB=1
∴AC=AF+FC=3
又∵Rt△ACD≌Rt△AED(HL或AAS)
∴AC=AE=3
∴AB=AE+EB=3+1=4
“点睛“此题考查了全等三角形的判定与性质,以及角平分线性质,熟练掌握全等三角形的判定与性质是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地某日最高气温27℃,最低15℃,最高气温比最低气温高( )
A. 22℃ B. 12℃ C. 15℃ D. 14℃
-
科目: 来源: 题型:
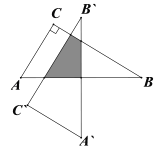
查看答案和解析>>【题目】如图,在Rt△ABC中,已知∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
证明:CF∥DO.

证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°( )
∴DE∥BO( )
∴∠EDO=∠DOF( )
又∵∠CFB=∠EDO( ④ )
∴∠DOF=∠CFB( ⑤ )
∴CF∥DO( ⑥ )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.
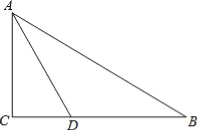
(1)动手操作:利用尺规作⊙O,使⊙O经过点A、D,且圆心O在AB上;并标出⊙O与AB的另一个交点E(保留作图痕迹,不写作法);
(2)综合应用:在你所作的图中,
①判断直线BC与⊙O的位置关系,并说明理由;
②若AB=6,BD=2
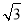 ,求线段BD、BE与劣弧
,求线段BD、BE与劣弧 所围成的图形面积(结果保留根号和π).
所围成的图形面积(结果保留根号和π). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在单位正方形网格中,建立了平面直角坐标系xOy,试解答下列问题:
(1)写出三角形ABC三个顶点的坐标;
(2)画出三角形ABC向右平移6个单位,再向下平移2个单位后的图形三角形DEF;
(3)若点P(a,b)是三角形ABC内部一点,求平移后三角形A,B,C,内的对应点P,的坐标.
(4)求三角形DEF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
相关试题

