【题目】如图,在⊙O中,AB是直径,CD是弦,AB⊥CD. 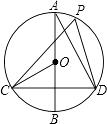
(1)P是 ![]() 上一点(不与C、D重合),求证:∠CPD=∠COB;
上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论.
参考答案:
【答案】
(1)证明:连接OD,
∵AB是直径,AB⊥CD,
∴ ![]() .
.
∴∠COB=∠DOB= ![]() ∠COD.
∠COD.
又∵∠CPD= ![]() ∠COD,
∠COD,
∴∠CPD=∠COB
(2)解:∠CP′D+∠COB=180°.
理由如下:连接OD,
∵∠CPD+∠CP′D=180°,∠COB=∠DOB= ![]() ∠COD,
∠COD,
又∵∠CPD= ![]() ∠COD,
∠COD,
∴∠COB=∠CPD,
∴∠CP′D+∠COB=180°.
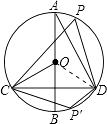
【解析】(1)根据垂径定理知,弧CD=2弧BC,由圆周角定理知,弧BC的度数等于∠BOC的度数,弧AD的度数等于∠CPD的2倍,可得:∠CPD=∠COB;(2)根据圆内接四边形的对角互补知,∠CP′D=180°﹣∠CPD,而:∠CPD=∠COB,∴∠CP′D+∠COB=180°.
【考点精析】解答此题的关键在于理解圆心角、弧、弦的关系的相关知识,掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.

(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶.下图是其中的甲、乙两段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
图中的数字表示每一级台阶的高度(单位:cm),并且数据15,16,16,14,14,15的方差s甲2=
 ,数据11,15,18,17,10,19的方差s乙2=
,数据11,15,18,17,10,19的方差s乙2= .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中真命题的个数( )
(1)已知直角三角形面积为4,两直角边的比为1:2,则它的斜边为5;
(2)直角三角形的最大边长为26,最短边长为10,则另一边长为24;
(3)在直角三角形中,两条直角边长为n2﹣1和2n,则斜边长为n2+1;
(4)等腰三角形面积为12,底边上的底为4,则腰长为5.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在网格中,小正方形边长为a,则图中是直角三角形的是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
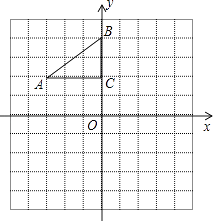
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利过程.下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:

(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润是多少万元?
相关试题

