【题目】如图,在网格中,小正方形边长为a,则图中是直角三角形的是_____.

参考答案:
【答案】直角三角形有两个,分别是△ABC与△DEF.
【解析】
根据已知及勾股定理的逆定理进行分析,从而得到答案.
解:∵小正方形的边长为a,
∴在△ABC中,
BC2=a2+(3a) 2=10a2,
AB2=AC2=a2+(2a) 2=5a2,
故BC2=AB2+AC2.
在△GKP中,
KG2=(2a)2+(2a)2=8a2,
GP2=a2+(2a) 2=5a2,KP2=(3a) 2=9a2,
KP2≠KG2+GP2.
在△DEF中,
DE2=(2a)2+(2a)2=8a2,
EF2=(3a)2+(3a)2=18a2,
DF2=a2+(5a)2=26a2,故DF2=DE2+EF2.
故直角三角形有两个,分别是△ABC与△DEF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶.下图是其中的甲、乙两段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
图中的数字表示每一级台阶的高度(单位:cm),并且数据15,16,16,14,14,15的方差s甲2=
 ,数据11,15,18,17,10,19的方差s乙2=
,数据11,15,18,17,10,19的方差s乙2= .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中真命题的个数( )
(1)已知直角三角形面积为4,两直角边的比为1:2,则它的斜边为5;
(2)直角三角形的最大边长为26,最短边长为10,则另一边长为24;
(3)在直角三角形中,两条直角边长为n2﹣1和2n,则斜边长为n2+1;
(4)等腰三角形面积为12,底边上的底为4,则腰长为5.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
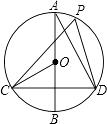
(1)P是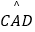 上一点(不与C、D重合),求证:∠CPD=∠COB;
上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
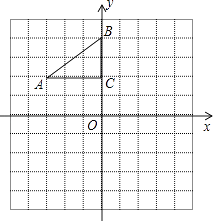
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利过程.下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:

(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润是多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】长城科技公司生产销售一种电子产品,该产品总成本包括技术成本、制造成本、销售成本三部分,经核算,2014年该产品各部分成本所占比例约为2:a:1.且2014年该产品的技术成本、制造成本分别为400万元、1400万元.
(1)确定a的值,并求2014年产品总成本为多少万元;
(2)为降低总成本,该公司2015年及2016年增加了技术成本投入,确保这两年技术成本都比前一年增加一个相同的百分数m(m<50%),制造成本在这两年里都比前一年减少一个相同的百分数2m;同时为了扩大销售量,2016年的销售成本将在2014年的基础上提高10%,经过以上变革,预计2016年该产品总成本达到2014年该产品总成本的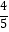 ,求m的值.
,求m的值.
相关试题

