【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
参考答案:
【答案】
(1)解:∵∠ACB=90°,AC=3,BC=4, ∴AB= ![]() =5.
=5.
∵AD=5t,CE=3t, ∴当AD=AB时,5t=5,即t=1;
∴AE=AC+CE=3+3t=6,DE=6﹣5=1
(2)解:∵EF=BC=4,G是EF的中点,
∴GE=2.
当AD<AE(即t< ![]() )时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,
)时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,
若△DEG与△ACB相似,则 ![]() 或
或 ![]() ,
,
∴ ![]() 或
或 ![]() ,
,
∴t= ![]() 或t=
或t= ![]() ;
;
当AD>AE(即t> ![]() )时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,
)时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,
若△DEG与△ACB相似,则 ![]() 或
或 ![]() , ∴
, ∴ ![]() 或
或 ![]() ,
,
解得t= ![]() 或t=
或t= ![]() ;
;
综上所述,当t= ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() 时,△DEG与△ACB相似
时,△DEG与△ACB相似
【解析】(1)先根据勾股定理求出AB的长,再根据点D的运动速度及AD=AB,求出t的值,然后根据点E的运动速度求出AE的长,从而可求出DE的长。
(2)根据EF=BC=4,G是EF的中点,求出GE的长,要证明△DEG与△ACB,分两种情况:DE:EG=BC:AC或DE:EG=AC:BC,根据这些线段成比例,即可求出t的值(注意点D的运动过程中,要分两种情况:AD<AE和AD>AE)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系,△ABC的三个顶点都在网格的格点上.
(1)把△ABC向下平移6个单位长度,再向左平移5个单位长度,得到△A1B1C1.请直接写出点A1、点B1和点C1的坐标.(不需要画图)
(2)求△ABC的面积.
(3)点D的坐标为(-3,1),在坐标轴上是否存在点E使得△BDE的面积等于△ABC的面积,若存在,请直接写出点E的坐标,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2.求证:∠3=∠ACB.
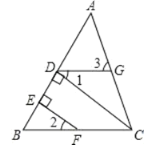
下面给出了部分证明过程和理由,请补全所有内容.
证明:∵CD⊥AB,FE⊥AB
∴∠BDC=∠BEF=90°( )
∴EF∥DC( )
∴∠2= ( )
又∵∠2=∠1(已知)
∴∠1= (等量代换)
∴DG∥BC( )
∴∠3=∠ACB(两直线平行,同位角相等)
-
科目: 来源: 题型:
查看答案和解析>>【题目】南湖公园有很多的长方形草地,草地里修了很多有趣的小路,下面三个图形都是长为50米,宽为30米的长方形草地,且小路的宽都是1米.
①如图1,阴影部分为1米宽的小路,长方形除去阴影部分后剩余部分为草地,则草地的面积为 ;
②如图2,有两条宽均为1米的小路(图中阴影部分),求草地的面积.
③如图3,非阴影部分为1米宽的小路,沿着小路的中间从入口E处走到出口F处,所走的路线(图中虚线)长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人从学校出发,沿相同的线路跑向公园.甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度继续跑向公园.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)之间函数关系的图象,根据题意填空:
(1)在跑步的全过程中,甲共跑了 米,甲的速度为 米/秒;
(2)乙最早出发时跑步的速度为 米/秒,乙在途中等候甲的时间为 秒;
(3)乙出发 秒后与甲第一次相遇.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A为
 边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sin
边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sin 的值,错误的是( )
的值,错误的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )
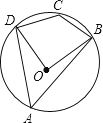
A.88°
B.92°
C.106°
D.136°
相关试题

