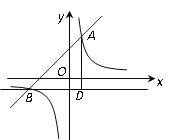
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A(1,3)和B(-3,
的图象交于点A(1,3)和B(-3, ![]() ).
).
(1)求一次函数和反比例函数的解析式;
(2)点C是平面直角坐标系内一点,BC∥![]() 轴,AD⊥BC于点D,连结AC,若
轴,AD⊥BC于点D,连结AC,若![]() ,求点C的坐标.
,求点C的坐标.
参考答案:
【答案】(1)反比例函数解析式为![]() ,一次函数解析式为
,一次函数解析式为![]() .(2)点C的坐标为C(-1,-1)或(3,-1).
.(2)点C的坐标为C(-1,-1)或(3,-1).
【解析】试题分析:(1)将点A坐标代入反比例函数![]() 中,得出k的值,再求出m的值,将A、B两点坐标代入一次函数中,求出a、b的值即可;(2)设点C的横坐标为x,
中,得出k的值,再求出m的值,将A、B两点坐标代入一次函数中,求出a、b的值即可;(2)设点C的横坐标为x,
根据点A(1,3)、B(-3,-1)得出CD、AD的长度,在Rt△ACD中,根据CD2+AD2=AC2,即可求出x的值,即可得点C的坐标;
试题解析:
(1)将点A(1,3)代入反比例函数解析式![]() 得,
得,
![]() ,
,
∴反比例函数解析式为![]() ,
,

∵A(1,3)和B(-3, ![]() )都在反比例函数的图象上,
)都在反比例函数的图象上,
∴![]() ,
,
解得: ![]() ,
,
∴B(-3,-1),
∵一次函数![]() 的图象经过A(1,3)和B(-3,-1),
的图象经过A(1,3)和B(-3,-1),
∴![]() ,
,
解得: ![]() ,
,
∴一次函数解析式为![]() .
.
(2)∵BC∥![]() 轴,AD⊥BC于点D,且A(1,3),B(-3,-1),设点C的横坐标为x,
轴,AD⊥BC于点D,且A(1,3),B(-3,-1),设点C的横坐标为x,
∴D(1,-1),C(![]() ,-1),
,-1),
∴![]() ,AD=4,
,AD=4,
∵![]() ,
,
∴在Rt△ACD中,有![]() ,
,
解得: ![]() ,
, ![]() ,
,
∴点C的坐标为C(-1,-1)或(3,-1).
-
科目: 来源: 题型:
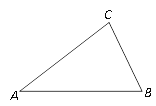
查看答案和解析>>【题目】如图,在△ABC中, AC=6, BC=4.
(1)用直尺和圆规作∠ACB的角平分线CD,交AB于点D;
(保留作图痕迹,不要求写作法和证明)
(2)在(1)所作的图形中,若△ACD的面积为3,求△BCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题.并证明这个命题(只写出一种情况)①AB=AC ②DE=DF ③BE=CF
已知:EG∥AF, , .
求证: .
证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项3x2y﹣4x3y3﹣9xy2﹣9按x的升幂排列为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.

(1)求证:MN=AM+BN.
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由. -
科目: 来源: 题型:
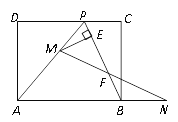
查看答案和解析>>【题目】如图,已知矩形ABCD的一条边AD=8 cm,点P在CD边上,AP=AB, PC=4cm,连结PB.点M从点P出发,沿PA方向匀速运动(点M与点P、A不重合);点N同时从点B出发,沿线段AB的延长线匀速运动,连结MN交PB于点F.
(1)求AB的长;
(2)若点M的运动速度为1cm/s,点N的运动速度为2cm/s,△AMN的面积为S,点M和点N的运动时间为
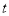 ,求S与
,求S与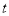 的函数关系式,并求S的最大值;
的函数关系式,并求S的最大值;(3)若点M和点N的运动速度相等,作ME⊥BP于点E.试问当点M、N在运动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程(a+1)x2+2x﹣1=0是一元二次方程,则a的取值范围是( )
A.a≠﹣1B.a>﹣1C.a<﹣1D.a≠0
相关试题

