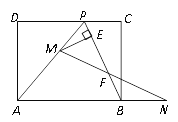
【题目】如图,已知矩形ABCD的一条边AD=8 cm,点P在CD边上,AP=AB, PC=4cm,连结PB.点M从点P出发,沿PA方向匀速运动(点M与点P、A不重合);点N同时从点B出发,沿线段AB的延长线匀速运动,连结MN交PB于点F.
(1)求AB的长;
(2)若点M的运动速度为1cm/s,点N的运动速度为2cm/s,△AMN的面积为S,点M和点N的运动时间为![]() ,求S与
,求S与![]() 的函数关系式,并求S的最大值;
的函数关系式,并求S的最大值;
(3)若点M和点N的运动速度相等,作ME⊥BP于点E.试问当点M、N在运动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
参考答案:
【答案】(1)10;(2)![]() 时,S取得最大值为45.(3)点M、N在运动过程中,线段EF的长度不变,长度为
时,S取得最大值为45.(3)点M、N在运动过程中,线段EF的长度不变,长度为![]() .
.
【解析】试题分析:(1)设AB=x,根据折叠可得AP=CD=x,DP=CD-CP=x-4,利用勾股定理,在Rt△ADP中,AD2+DP2=AP2,即82+(x-4)2=x2,即可解答;(2)过点M作MG⊥AN于点G,则∠AGM=∠D=90°,所以∠APD=∠MAG,则Rt△APD∽Rt△MAG,所以![]() ,即
,即![]() ,可得出
,可得出![]() , 又因为
, 又因为![]() ,所以
,所以![]()
![]()
![]() ,则当
,则当![]() 时,S取得最大值为45;(3)作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据MH⊥PQ,得出HQ=
时,S取得最大值为45;(3)作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据MH⊥PQ,得出HQ=![]() PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=
PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=![]() QB,再求出EF=
QB,再求出EF=![]() PB,最后代入HF=
PB,最后代入HF=![]() PB即可得出线段EF的长度不变;
PB即可得出线段EF的长度不变;
试题解析:
(1)设AB= ![]() ,则AP=
,则AP= ![]() ,DP=
,DP= ![]() ,
,
在Rt△ADP中, 由勾股定理得:
![]() ,
,
解得: ![]() ,
,
∴AB =10.
(2)过点M作MG⊥AN于点G,则∠AGM=∠D=90°,
∵DC∥AB,
∴∠APD=∠MAG,
∴Rt△APD∽Rt△MAG,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
![]()
![]()
∴当![]() 时,S取得最大值为45.
时,S取得最大值为45.
(3)作MQ∥AN,交PB于点Q,
∵AP=AB,MQ∥AN,
∴∠APB=∠ABP,∠ABP=∠MQP,
∴∠APB=∠MQP,
∴MP=MQ,
∵ME⊥PQ,
∴PE=EQ=![]() PQ,
PQ,
∵BN=PM,PM=MQ,
∴BN=QM,
∵MQ∥AN,∴∠QMF=∠BNF,
在△MFQ和△NFB中,
∵ ,
,
∴△MFQ≌△NFB,
∴QF=BF,
∴QF=![]() QB,
QB,
∴EF=EQ+QF=![]() PQ+
PQ+![]() QB=
QB=![]() PB,
PB,
在Rt△PBC中,
∵PC=4,BC=8,
∴![]() ,
,
∴EF=![]() PB=
PB=![]() ,
,
∴点M、N在运动过程中,线段EF的长度不变,长度为![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项3x2y﹣4x3y3﹣9xy2﹣9按x的升幂排列为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
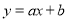 的图象与反比例函数
的图象与反比例函数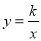 的图象交于点A(1,3)和B(-3,
的图象交于点A(1,3)和B(-3, 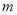 ).
).(1)求一次函数和反比例函数的解析式;
(2)点C是平面直角坐标系内一点,BC∥
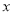 轴,AD⊥BC于点D,连结AC,若
轴,AD⊥BC于点D,连结AC,若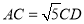 ,求点C的坐标.
,求点C的坐标.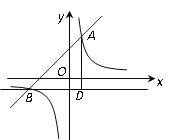
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.

(1)求证:MN=AM+BN.
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程(a+1)x2+2x﹣1=0是一元二次方程,则a的取值范围是( )
A.a≠﹣1B.a>﹣1C.a<﹣1D.a≠0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
(1)求证:AE是⊙O的切线;
(2)若AB=AD,AC=
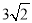 ,tan∠ADC=3,求BE的长.
,tan∠ADC=3,求BE的长.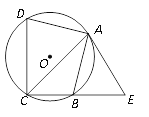
-
科目: 来源: 题型:
查看答案和解析>>【题目】荔枝是岭南一带的特色时令水果.今年5月份荔枝一上市,某水果店的老板用3000元购进了一批荔枝,由于荔枝刚在果园采摘比较新鲜,前两天他以高于进价40% 的价格共卖出150千克,由于荔枝保鲜期短,第三天他发现店里的荔枝卖相已不大好,于是果断地将剩余荔枝以低于进价20%的价格全部售出,前后一共获利750元.
(1)若购进的荔枝为
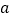 千克,则这批荔枝的进货价为 ;(用含
千克,则这批荔枝的进货价为 ;(用含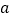 的式子来表示)
的式子来表示)(2)求该水果店的老板这次购进荔枝多少千克.
相关试题

