【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D. 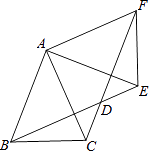
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
参考答案:
【答案】
(1)证明:∵△AEF是由△ABC绕点A按逆时针方向旋转得到的,
∴AE=AF=AB=AC=2,∠EAF=∠BAC=45°,
∴∠BAC+∠3=∠EAF+∠3,即∠BAE=∠CAF,
在△ABE和△ACF中
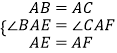 ,
,
∴△ABE≌△ACF,
∴BE=CF
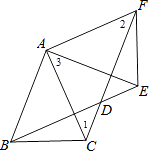
(2)解:∵四边形ABDF为菱形,
∴DF=AF=2,DF∥AB,
∴∠1=∠BAC=45°,
∴△ACF为等腰直角三角形,
∴CF= ![]() AF=2
AF=2 ![]() ,
,
∴CD=CF﹣DF=2 ![]() ﹣2.
﹣2.
【解析】(1)根据旋转的性质得AE=AF=AB=AC=2,∠EAF=∠BAC=45°,然后根据“SAS”证明△ABE≌△ACF,于是根据全等三角形的性质即可得到结论;(2)根据菱形的性质得DF=AF=2,DF∥AB,再利用平行线的性质得∠1=∠BAC=45°,则可判断△ACF为等腰直角三角形,所以CF= ![]() AF=2
AF=2 ![]() ,然后计算CF﹣DF即可.
,然后计算CF﹣DF即可.
【考点精析】通过灵活运用菱形的性质和旋转的性质,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,分别平行x,y轴的两直线a,b相交于点A(3,4).连接OA,若在直线a上存在点P,使△AOP是等腰三角形,那么所有满足条件的点P的坐标是___

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
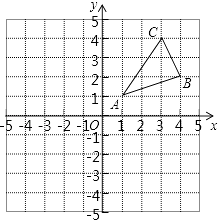 .
.
(1)请画出△ABC关于原点对称的△A2B2C2;并写出各点的坐标.
(2)在x轴上求作一点P,使△PAB的周小最小,请画出△PAB,并直接写出P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】以x为自变量的二次函数y=﹣x2+(2m+2)x﹣(m2+4m﹣3)中,m为不小于0的整数,它的图象与x轴的交点A在原点左边,交点B在原点右边.
(1)求这个二次函数的解析式;
(2)设点C为此二次函数图象上的一点,且满足△ABC的面积等于10,请求出点C的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于概率,下列说法正确的是( )
A.莒县“明天降雨的概率是75%”表明明天莒县会有75%的时间会下雨
B.随机抛掷一枚质地均匀的硬币,落地后一定反面向上
C.在一次抽奖活动中,中奖的概率是1%,则抽奖100次就一定会中奖
D.同时抛掷两枚质地均匀硬币,“一枚硬币正面向上,一枚硬币反面向上”的概率是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形BCO是三角形BAO经过某种变换得到的.
(1)写出A,C的坐标;
(2)图中A与C的坐标之间的关系是什么?
(3)如果三角形AOB中任意一点M的坐标为(x,y),那么它的对应点N的坐标是什么?

相关试题

