【题目】以x为自变量的二次函数y=﹣x2+(2m+2)x﹣(m2+4m﹣3)中,m为不小于0的整数,它的图象与x轴的交点A在原点左边,交点B在原点右边.
(1)求这个二次函数的解析式;
(2)设点C为此二次函数图象上的一点,且满足△ABC的面积等于10,请求出点C的坐标.
参考答案:
【答案】
(1)解:∵图象与x轴的交点A在原点左边,交点B在原点右边,
∴△=(2m+2)2﹣4×(﹣1)×[﹣(m2+4m﹣3)]>0,
解得:m<2,
∵m为不小于0的整,
∴m=0或1.
当m=0时,y=﹣x2+2x+3,其中A(﹣1,0),B(3,0);
当m=1时,y=﹣x2+4x﹣2,不合题意;
∴二次函数的解析式为:y=﹣x2+2x+3
(2)解:∵△ABC的面积等于10,|AB|=4,
∴ ![]() |AB|h=10,
|AB|h=10,
∴h=5,
∴C点的纵坐标为5或﹣5,
当C点的纵坐标为5时,﹣x2+2x+3=5,即﹣x2+2x﹣2=0,△=4﹣4×(﹣1)×(﹣2)<0,不合题意,舍去;
当C点的纵坐标为﹣5时,﹣x2+2x+3=﹣5,即﹣x2+2x+8=0,
解得:x=4或﹣2,
所以点C的坐标为:(4,﹣5)或(﹣2,﹣5)
【解析】(1)由二次函数y=﹣x2+(2m+2)x﹣(m2+4m﹣3)中,m为不小于0的整数,它的图象与x轴的交点A在原点左边,交点B在原点右边,可确定m的值,可得二次函数的解析式;(2)由△ABC的面积等于10,|AB|=4,求出点C的纵坐标,再代入解析式可得点C的横坐标,即得点C的坐标.
【考点精析】关于本题考查的抛物线与坐标轴的交点,需要了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.
-
科目: 来源: 题型:
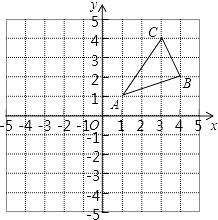
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
 .
.
(1)请画出△ABC关于原点对称的△A2B2C2;并写出各点的坐标.
(2)在x轴上求作一点P,使△PAB的周小最小,请画出△PAB,并直接写出P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,∠XOY=90°,点A、B分别在射线OX、OY上移动,BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D.
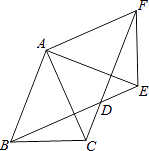
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=ax2﹣b与y=ax+b(ab≠0)的图象大致如图( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
①ac<0 ②2a+b=0 ③4a+2b+c>0 ④对任意实数x均有ax2+bx≥a+b
正确的结论序号为: .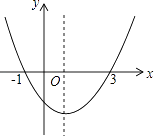
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了
 ,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
相关试题

