【题目】如图,在平面直角坐标系xOy中,分别平行x,y轴的两直线a,b相交于点A(3,4).连接OA,若在直线a上存在点P,使△AOP是等腰三角形,那么所有满足条件的点P的坐标是___

参考答案:
【答案】(8,4)或(-2,4)或(-3,4)或(-![]() ,4)
,4)
【解析】
根据题意可得0A=5,再分两种情况讨论:OA为等腰三角形一条腰;OA为底边.再计算求解.
∵A(3,4),
∴OB=3,AB=4,
∴0A=![]() =5,
=5,
①若AP=OA,则点P的坐标为:(8,4)或(-2,4),
②若AP=OP,设点P的坐标为:(x,4),
则(x-3)2=x2+42,
解得:x=-![]() ,
,
∴点P的坐标为(-![]() ,4);
,4);
③若OA=OP,设P的坐标为(x,4),
则x2+42=52,
解得:x=±3,
∴点P的坐标为:(-3,4);
∴所有满足条件的点P的坐标是:(8,4)或(-2,4)或(-![]() ,4)或(-3,4).
,4)或(-3,4).

故答案是:(8,4)或(-2,4)或(-![]() ,4)或(-3,4).
,4)或(-3,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京.已知A车的平均速度比B车的平均速度慢80km/h,A车的行驶时间比B车的行驶时间多40%,两车的行驶时间分别为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象经过点(﹣1,0)、(5,0)、(0、﹣5).
(1)求此二次函数的解析式;
(2)当0≤x≤5时,求此函数的最小值与最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
-
科目: 来源: 题型:
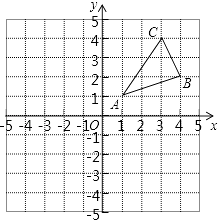
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
 .
.
(1)请画出△ABC关于原点对称的△A2B2C2;并写出各点的坐标.
(2)在x轴上求作一点P,使△PAB的周小最小,请画出△PAB,并直接写出P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D.
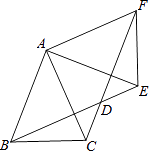
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】以x为自变量的二次函数y=﹣x2+(2m+2)x﹣(m2+4m﹣3)中,m为不小于0的整数,它的图象与x轴的交点A在原点左边,交点B在原点右边.
(1)求这个二次函数的解析式;
(2)设点C为此二次函数图象上的一点,且满足△ABC的面积等于10,请求出点C的坐标.
相关试题

