【题目】已知AB是⊙O的直径,⊙O过BC的中点D,且DE垂直AC于E.
(1)求证:AB=AC;
(2)求证:DE是⊙O的切线;
(3)若AB=13,BC=10,求DE的长

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)连结AD,如图,由圆周角定理得到∠ADB=90°,则AD⊥BC,加上BD=CD,即AD垂直平分BC,所以AB=AC;
(2)连结OD,如图,先证明OD为△ABC的中位线,根据三角形中位线性质得OD∥AC,而DE⊥AC,所以OD⊥DE,于是根据切线的判定定理可得DE是⊙O的切线;
(3)易得BD=DC=![]() BC=5,AC=AB=13,由勾股定理得到AD=12,再用面积法求出DE的长.
BC=5,AC=AB=13,由勾股定理得到AD=12,再用面积法求出DE的长.
试题解析:解:(1)连结AD,如图,∵AB为⊙O的直径,∴∠ADB=90°,∴AD⊥BC,∴D为BC的中点,∴BD=CD,∴AB=AC;
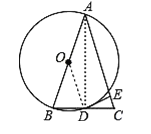
(2)连结OD,如图,∵OA=OB,DB=DC,∴OD为△ABC的中位线,∴OD∥AC,∵DE⊥AC,∴OD⊥DE,∴DE是⊙O的切线;
(3)BD=DC= ![]() BC=5,AC=AB=13,由勾股定理得:AD=12,在Rt△DAC中,
BC=5,AC=AB=13,由勾股定理得:AD=12,在Rt△DAC中, ![]() AD*DC=
AD*DC=![]() AC*DE,∴DE=
AC*DE,∴DE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用工件槽(如图1)可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A、B、E三个接触点,该球的大小就符合要求.图2是过球心O及A、B、E三点的截面示意图,求这种铁球的直径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=8,点E、F分别在AD和AB上,AE=3,AF=4.



(1)点P在边BC上运动、四边形EFPH是平行四边形,连接DH.
①当四边形FPHE是菱形时,线段BP=_____;
②当点P在边BC上运动时,△DEH的面积会不会变化?若变化,求其最大值;若不变,求出它的值;
③当△DEH是等腰三角形时,求BP的长;
(2)若点E沿E-D-C向终点C运动,点F沿F-B-C终点C运动,速度分别为每秒3个单位长度和每秒4个单位长度,当其中一个点到达终点C时,另一个点也停止运动,求EF的中点O的运动路径长(要求写出简略的计算过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小王某天下午营运是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6.
(1)将最后一名乘客送到目的地时,小王距下午出车时的出发点多远?
(2)若汽车耗油量为0.05升/千米,这天下午小王的汽车共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店出售
 、
、 两种文具.
两种文具. 文具每套
文具每套 元,
元, 文具每套
文具每套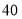 元,该店开展促销活动,向客户提供两种优惠方案:
元,该店开展促销活动,向客户提供两种优惠方案:①买一套
 文具送一套
文具送一套 文具.
文具.②
 文具和
文具和 文具都按定价的
文具都按定价的 付款.
付款.现某客户要到该店购买
 文具
文具 套,
套, 文具
文具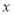 套(
套( )
)(
 )若该客户按方案①购买需付款____________________元(用含
)若该客户按方案①购买需付款____________________元(用含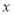 的代数式表示);若该客户按方案②购买需付款____________________元(用含
的代数式表示);若该客户按方案②购买需付款____________________元(用含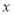 的代数式表示)
的代数式表示)(
 )当
)当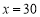 时,通过计算说明按哪种方案购买较为合算.
时,通过计算说明按哪种方案购买较为合算. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )

A.23°B.92°C.44°D.46°
相关试题

