【题目】某文具店出售![]() 、
、![]() 两种文具.
两种文具.![]() 文具每套
文具每套![]() 元,
元,![]() 文具每套
文具每套![]() 元,该店开展促销活动,向客户提供两种优惠方案:
元,该店开展促销活动,向客户提供两种优惠方案:
①买一套![]() 文具送一套
文具送一套![]() 文具.
文具.
②![]() 文具和
文具和![]() 文具都按定价的
文具都按定价的![]() 付款.
付款.
现某客户要到该店购买![]() 文具
文具![]() 套,
套,![]() 文具
文具![]() 套(
套(![]() )
)
(![]() )若该客户按方案①购买需付款____________________元(用含
)若该客户按方案①购买需付款____________________元(用含![]() 的代数式表示);若该客户按方案②购买需付款____________________元(用含
的代数式表示);若该客户按方案②购买需付款____________________元(用含![]() 的代数式表示)
的代数式表示)
(![]() )当
)当![]() 时,通过计算说明按哪种方案购买较为合算.
时,通过计算说明按哪种方案购买较为合算.
参考答案:
【答案】(1)3200+40x;3600+36x;(2) 当x=30时,选择方案①购买更合算
【解析】
(1)根据题中所给的两种方案分别列出代数式即可;
(2)把x=30代入(1)中式子进行解答即可.
(1)该客户按方案①购买需付款:200×20+(x-20)×40=3200+40x;
该客户按方案②购买需付款:200×20×0.9+40x×0.9=3600+36x;
(2)当x=30时,按方案①购买需付款:3200+40×30=4400(元);
按方案②购买需付款:3600+36×30=4680(元);
答:当x=30时,选择方案①购买更合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小王某天下午营运是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6.
(1)将最后一名乘客送到目的地时,小王距下午出车时的出发点多远?
(2)若汽车耗油量为0.05升/千米,这天下午小王的汽车共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,⊙O过BC的中点D,且DE垂直AC于E.
(1)求证:AB=AC;
(2)求证:DE是⊙O的切线;
(3)若AB=13,BC=10,求DE的长

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )

A.23°B.92°C.44°D.46°
-
科目: 来源: 题型:
查看答案和解析>>【题目】材料:在学习绝对值时,老师教过我们绝对值的几何含义,
 表示
表示 、
、 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离; ,所以
,所以 表示
表示 、
、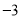 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离; ,所以
,所以 表示
表示 在数轴上对应的点到原点的距离,一般地,点
在数轴上对应的点到原点的距离,一般地,点 、
、 在数轴上分别表示有理数
在数轴上分别表示有理数 、
、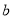 ,那么
,那么 、
、 之间的距离可表示为
之间的距离可表示为 .
.(
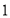 )点
)点 、
、 、
、 在数轴上分别表示有理数
在数轴上分别表示有理数 、
、 、
、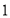 ,那么
,那么 到
到 的距离表示为______________________________(用含绝对值的式子表示).如果
的距离表示为______________________________(用含绝对值的式子表示).如果 ,那么
,那么 为______________________________.
为______________________________.(
 )利用数轴探究:
)利用数轴探究:①找出满足
 的
的 的所有整数值是____________________;
的所有整数值是____________________;②设
 ,当
,当 的值取在不小于
的值取在不小于 且不大于
且不大于 的范围时,
的范围时, 的值是不变的,而且是
的值是不变的,而且是 的最小值,这个最小值是____________________;
的最小值,这个最小值是____________________;(
 )求
)求 的最小值为____________________,此时
的最小值为____________________,此时 的值为____________________.
的值为____________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
相关试题

