【题目】如图,直线AE与CD相交于点B,射线BF平分∠ABC,射线BG在∠ABD内,
(1)若∠DBE的补角是它的余角的3倍,求∠DBE的度数;
(2)在(1)的件下,若∠DBG=∠ABG﹣33°,求∠ABG的度数;
(3)若∠FBG=100°,求∠ABG和∠DBG的度数的差.

参考答案:
【答案】(1)∠DBE的度数为45°;(2)∠ABG的度数为84°;(3)∠ABG和∠DBG的度数的差为20°.
【解析】
(1)设∠DBE=α,则∠DBE的补角是![]() ,它的余角是
,它的余角是![]() 依据
依据![]() 的补角是它的余角的3倍,即可得到方程,求得
的补角是它的余角的3倍,即可得到方程,求得![]() 的度数;
的度数;
(2)设∠ABG=x,∠DBG=y,依题意得得到方程组,即可得到∠ABG的度数;
(3)可设∠ABF=∠CBF=β,依据![]() 即可得到
即可得到![]()
![]() 依据
依据![]() 可得∠ABG和∠DBG的度数的差为
可得∠ABG和∠DBG的度数的差为![]() .
.
(1)设∠DBE=α,则∠DBE的补角是![]() ,它的余角是
,它的余角是![]() 依题意得
依题意得
![]()
解得![]()
∴∠DBE的度数为![]()
(2)设∠ABG=x,∠DBG=y,依题意得
![]() 解得
解得![]()
∴∠ABG的度数为![]()
(3)∵射线BF平分∠ABC,
∴可设∠ABF=∠CBF=β,
又∵![]()
∴![]()
∴![]()
即∠ABG和∠DBG的度数的差为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司今年销售一种产品,1月份获得利润20万元.由于产品畅销.利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.设这个增长率为x
(1)填空:(用含x的代数式表示)
①2月份的利润为:______
②3月份的利润为:______
(2)列出方程,并求出问题的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.
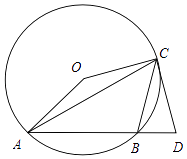
(1)求证:CD=CB;
(2)如果⊙O的半径为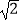 ,求AB的长.
,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校要围一个矩形花圃,其一边利用足够长的墙,另三边用篱笆围成,由于园艺需要,还要用一段篱笆将花圃分隔为两个小矩形部分(如图所示),总共36米的篱笆恰好用完(不考虑损耗).设矩形垂直于墙面的一边AB的长为x米(要求AB<AD),矩形花圃ABCD的面积为S平方米.

(1)求S与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)要想使矩形花圃ABCD的面积最大,AB边的长应为多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果方程x2+px+q=0的两个根是x1、x2,那么x1+x2=-p,x1x2=q,请根据以上结论,解决下列问题:
(1)已知x1、x2是方程x2+4x-2=0的两个实数根,求
 +
+ 的值;
的值;(2)已知方程x2+bx+c=0的两根分别为
 +1、
+1、 -1,求出b、c的值;
-1,求出b、c的值;(3)关于x的方程x2+(m-1)x+m2-3=0的两个实数根互为倒数,求m的值.
-
科目: 来源: 题型:
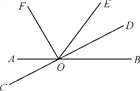
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线AB:y=5x﹣5与x轴交于点A,与y轴交于点B,点C与点B关于原点O对称,抛物线y=ax2+bx+c的对称轴为直线x=3且过点A和C.
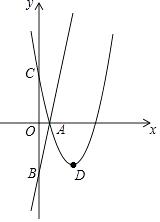
(1)求点A和点C的坐标;
(2)求抛物线y=ax2+bx+c的解析式;
(3)若抛物线y=ax2+bx+c的顶点为D,且在x轴上存在点P使得△DAP的面积为6,直接写出满足条件的点P的坐标.
相关试题

