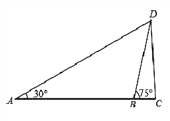
【题目】如图,为了测出某塔![]() 的高度,在塔前的平地上选择一点
的高度,在塔前的平地上选择一点![]() ,用测角仪测得塔顶
,用测角仪测得塔顶![]() 的仰角为
的仰角为![]() ,在
,在![]() 、
、![]() 之间选择一点
之间选择一点![]() (
(![]() 、
、![]() 、
、![]() 三点在同一直线上)用测角仪测得塔顶
三点在同一直线上)用测角仪测得塔顶![]() 的仰角为
的仰角为![]() ,且
,且![]() 间的距离为40m.
间的距离为40m.
(1)求点![]() 到
到![]() 的距离;
的距离;
(2)求塔高![]() (结果精确到0.1m.)(己知
(结果精确到0.1m.)(己知![]() ).
).
参考答案:
【答案】(1)点B到AD的距离为20m;(2)塔高CD为27.3m.
【解析】分析:(1)过点B作BE⊥AD于点E,然后根据AB=40m,∠A=30°,可求得点B到AD的距离。
(2)先求出∠EBD的度数,然后求出AD的长度,然后根据∠A=30°即可求出CD的高度。
详解:(1)过点B作BE⊥AD于点E,
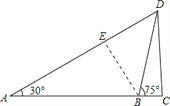
∵AB=40m,∠A=30°,
∴BE=![]() AB=20m,AE=
AB=20m,AE=![]() m,
m,
即点B到AD的距离为20m;
(2)在Rt△ABE中,
∵∠A=30°,∴∠ABE=60°,
∵∠DBC=75°,∴∠EBD=180°-60°-75°=45°,∴DE=EB=20m,
则AD=AE+EB=20![]() +20=20(
+20=20(![]() +1),
+1),
在Rt△ADC中,∠A=30°, ∴DC=![]() =10+10
=10+10![]() =27.3
=27.3
答:塔高CD为27.3m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将口ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,C,D是直线AB上的两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.
(1)猜想:CE和DF是否平行?请说明理由;
(2)若∠DCE=130°,求∠DEF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】中国移动公司开设适合普通用户的两种通讯业务分别是:“全球通”用户先缴
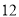 元月租,然后每分钟通话费用
元月租,然后每分钟通话费用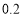 元;“神州行”用户不用缴纳月租费,每分钟通话
元;“神州行”用户不用缴纳月租费,每分钟通话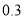 元.(通话均指拨打本地电话)
元.(通话均指拨打本地电话)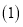 设一个月内通话时间约为
设一个月内通话时间约为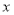 分钟(
分钟(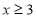 且
且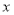 为整数),求这两种用户每月需缴的费用分别是多少元?(用含
为整数),求这两种用户每月需缴的费用分别是多少元?(用含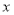 的式子表示)
的式子表示) 若张老师一个月通话约
若张老师一个月通话约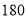 分钟,请你给他提个建议,应选择哪种移动通讯方式合算一些?并说明理由.
分钟,请你给他提个建议,应选择哪种移动通讯方式合算一些?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放
 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
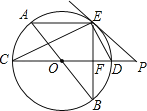
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一对数,如下表,第
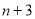 个数比第n个数大2(其中n是正整数)
个数比第n个数大2(其中n是正整数)第1个
第2个
第3个
第4个
第5个
……
a
b
c
(1)第5个数表示为______;第7个数表示为_______.
(2)若第10个数是5,第11个数是8,第12个数为9,则a=______,b=_____,c=______.
(3)第2019个数可表示为________.
相关试题

