【题目】有这样一对数,如下表,第![]() 个数比第n个数大2(其中n是正整数)
个数比第n个数大2(其中n是正整数)
第1个 | 第2个 | 第3个 | 第4个 | 第5个 | …… |
a | b | c |
(1)第5个数表示为______;第7个数表示为_______.
(2)若第10个数是5,第11个数是8,第12个数为9,则a=______,b=_____,c=______.
(3)第2019个数可表示为________.
参考答案:
【答案】(1)b+2,a+4;(2)-1,2,3;(3)c+1344
【解析】
根据要求将第1个至第12个数都表示出来,再利用对应相等的量求出a、b、c的值,由此得到规律,从而求出第2019个数.
第1个至第12个数见表:
第1个 | 第2个 | 第3个 | 第4个 | 第5个 | 第6个 | 第7个 | 第8个 | 第9个 | 第10个 | 第11个 | 第12个 |
a | b | c | a+2 | b+2 | c+2 | a+4 | b+4 | c+4 | a+6 | b+6 | c+6 |
所以(1)填b+2;a+4;
(2)由表得a+6=5,b+6=8,c+6=9
∴a=-1,b=2,c=3;
(3)由表可知,每三个数是一组变化,能被3整除的个数可以表示为c+2(![]() -1)
-1)
而2019能被3整除,所以第2019个数可表示为c+1344
-
科目: 来源: 题型:
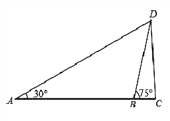
查看答案和解析>>【题目】如图,为了测出某塔
 的高度,在塔前的平地上选择一点
的高度,在塔前的平地上选择一点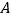 ,用测角仪测得塔顶
,用测角仪测得塔顶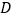 的仰角为
的仰角为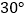 ,在
,在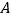 、
、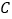 之间选择一点
之间选择一点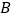 (
(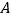 、
、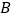 、
、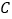 三点在同一直线上)用测角仪测得塔顶
三点在同一直线上)用测角仪测得塔顶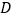 的仰角为
的仰角为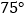 ,且
,且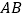 间的距离为40m.
间的距离为40m.(1)求点
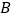 到
到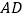 的距离;
的距离; (2)求塔高
 (结果精确到0.1m.)(己知
(结果精确到0.1m.)(己知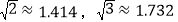 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放
 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值. -
科目: 来源: 题型:
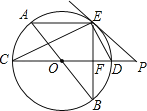
查看答案和解析>>【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线
 与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.
与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.(1)直接写出
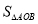 = ;
= ;(2)请你过点C作CE⊥y轴于E点,试探究OB+OA与CE的数量关系,并证明你的结论;
(3)若点M为AB的中点,点N为OC的中点,求MN的值;
(4)如图2,将线段AB绕点B沿顺时针方向旋转至BD,且OD⊥AD,延长DO交直线
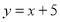 于点P,求点P的坐标.
于点P,求点P的坐标.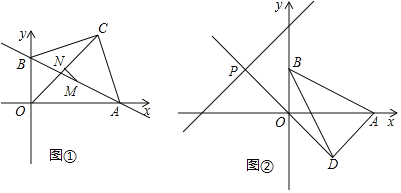
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
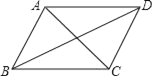
A. 当AB=BC时四边形ABCD是菱形
B. 当AC⊥BD时四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD且∠ABC=90°时四边形ABCD是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )

A.
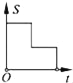 B.
B. 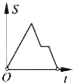 C.
C. 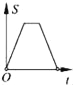 D.
D. 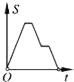
相关试题

