【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:CD平分∠ECA.
(2)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.

参考答案:
【答案】(1)见解析;(2)∠BDC=![]() ∠BAC,见解析.
∠BAC,见解析.
【解析】
(1)根据平行线的性质得到∠ADB=∠DBC,由角平分线的定义得到∠ABD=∠DBC,等量代换得到∠ABD=∠ADB,根据等腰三角形的判定即可得到AB=AD根据平行线的性质得到∠ADC=∠DCE,由①知AB=AD,等量代换得到AC=AD,根据等腰三角形的性质得到∠ACD=∠ADC,求得∠ACD=∠DCE,即可得到结论;
(2)根据角平分线的定义得到∠DBC=![]() ∠ABC,∠DCE=
∠ABC,∠DCE=![]() ∠ACE,由于∠BDC+∠DBC=∠DCE于是得到∠BDC+
∠ACE,由于∠BDC+∠DBC=∠DCE于是得到∠BDC+![]() ∠ABC=∠ACE,由∠BAC+∠ABC=∠ACE,于是得到∠DC+
∠ABC=∠ACE,由∠BAC+∠ABC=∠ACE,于是得到∠DC+![]() ∠ABC=
∠ABC=![]() ∠ABC+
∠ABC+![]() ∠BAC,即可得到结论.
∠BAC,即可得到结论.
(1)∵AD∥BE,
∴∠ADB=∠DBC,∵BD平分∠ABC,
∴∠ABD=∠DBC,∴∠ABD=∠ADB,
∴AB=AD;
又∵AD∥BE,∴∠ADC=∠DCE,
又∵AB=AC,AB=AD,
∴AC=AD,∴∠ACD=∠ADC,
∴∠ACD=∠DCE,
∴CD平分∠ACE;
(2)∠BDC=![]() ∠BAC,
∠BAC,
∵BD、CD分别平分∠ABE,∠ACE,
∴∠DBC=![]() ∠ABC,∠DCE=
∠ABC,∠DCE=![]() ∠ACE,
∠ACE,
∵∠BDC+∠DBC=∠DCE,
∴∠BDC+![]() ∠ABC=
∠ABC=![]() ∠ACE,
∠ACE,
∵∠BAC+∠ABC=∠ACE,
∴∠BDC+![]() ∠ABC=
∠ABC=![]() ∠ABC+
∠ABC+![]() ∠BAC,
∠BAC,
∴∠BDC=![]() ∠BAC.
∠BAC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强打算找印刷公司设计一款新年贺卡并印刷.如图1是甲印刷公司设计与印刷卡片计价方式的说明(包含设计费与印刷费),乙公司的收费与印刷卡片数量的关系如图2所示.
(1)分别写出甲乙两公司的收费y(元)与印刷数量x之间的关系式.
(2)如果你是小强,你会选择哪家公司?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小英、小丽、小华的家位于同一直线上,已知小明家(A)与小英家(B)的距离为320米,小丽家(C)与小英家(B)的距离为480米,小华家(D)位于小明家(A)与小丽家(C)中间的位置.请你根据条件,画出图形,求出小明家(A)与小华家(D)的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,
 D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且
D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且 连接EF并取EF的中点O,连接DO并延长至点G,使
连接EF并取EF的中点O,连接DO并延长至点G,使 ,连接DE,DF,GE,GF
,连接DE,DF,GE,GF
(1)求证:四边形EDFG是正方形;
(2)直接写出当点E在什么位置时,四边形EDFG的面积最小?最小值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1.正方形ABCD,过点A作∠EAF=90°,两边分别交直线BC于点E,交线段CD于点F,G为AE中点,连接BG
(1)求证:△ABE≌△ADF
(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB;
(3)如图3,连接HF,若CH=3AH,AD=2
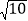 ,求线段HF的长.
,求线段HF的长.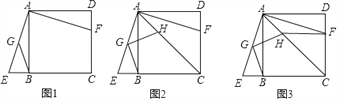
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场投入
 元资金购进甲、乙两种矿泉水共
元资金购进甲、乙两种矿泉水共 箱,矿泉水的成本价和销售价如表所示:
箱,矿泉水的成本价和销售价如表所示:(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完
 箱矿泉水,该商场共获得利润多少元?
箱矿泉水,该商场共获得利润多少元?类别
成本价(元/箱)
销售价(元/箱)
甲


乙


-
科目: 来源: 题型:
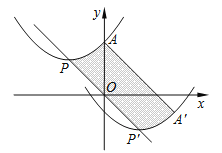
查看答案和解析>>【题目】如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为______.
相关试题

