【题目】如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.
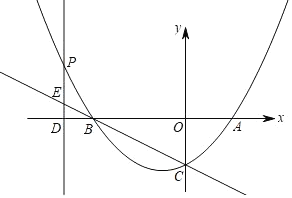
(1)求抛物线的函数表达式;
(2)若点P在第二象限内,且PE=![]() OD,求△PBE的面积.
OD,求△PBE的面积.
(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=![]() x2+
x2+![]() x﹣2;(2)
x﹣2;(2)![]() ;(3)M坐标为(
;(3)M坐标为(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
【解析】
(1)点A(2,0)、点B(-4,0),则函数的表达式为:y=a(x-2)(x+4)=a(x2+2x-8),即可求解;
(2)PE=![]() OD,则PE=(
OD,则PE=(![]() x2+
x2+![]() x-2-
x-2-![]() x+2)=
x+2)=![]() (-x),求得:点D(-5,0),利用S△PBE=
(-x),求得:点D(-5,0),利用S△PBE=![]() PE×BD=
PE×BD=![]() (
(![]() x2+
x2+![]() x-2-
x-2-![]() x+2)(-4-x),即可求解;
x+2)(-4-x),即可求解;
(3)分两种情况求解即可:①当BD=BM时,②当BD=DM(M′)时.
(1)点A的坐标是(2,0),抛物线的对称轴是直线x=﹣1,则点B(﹣4,0),
则函数的表达式为:y=a(x﹣2)(x+4)=a(x2+2x﹣8),
把点C(0,-2)代入得:﹣8a=﹣2,解得:a=![]() ,
,
故抛物线的表达式为:y=![]() x2+
x2+![]() x﹣2;
x﹣2;
(2)将点B、C的坐标代入一次函数表达式:y=mx+n并解得:
直线BC的表达式为:y=﹣![]() x﹣2,则tan∠ABC=
x﹣2,则tan∠ABC=![]() ,则sin∠ABC=
,则sin∠ABC=![]() ,
,
设点D(x,0),则点P(x,![]() x2+
x2+![]() x﹣2),点E(x,﹣
x﹣2),点E(x,﹣![]() x﹣2),
x﹣2),
∵PE=![]() OD,OD=﹣x,
OD,OD=﹣x,
∴PE=(![]() x2+
x2+![]() x﹣2+
x﹣2+![]() x+2)=
x+2)=![]() x2+x,
x2+x,
即![]() x2+x=-
x2+x=-![]() x,
x,
解得:x=0或﹣5(舍去x=0),
即点D(﹣5,0),
S△PBE=![]() ×PE×BD=
×PE×BD=![]() (
(![]() x2+
x2+![]() x﹣2+
x﹣2+![]() x+2)(﹣4﹣x)=
x+2)(﹣4﹣x)=![]() ;
;
(3)由题意得:△BDM是以BD为腰的等腰三角形,
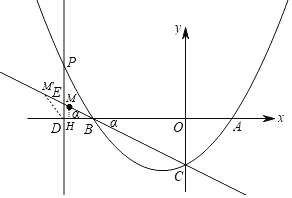
①当BD=BM时,过点M作MH⊥x轴于点H,
BD=1=BM,
则MH=yM=BMsin∠ABC=1×![]() =
=![]() ,
,
则xM=![]() ,
,
故点M(![]() ,
,![]() );
);
②当BD=DM(M′)时,
同理可得:点M′(﹣![]() ,
,![]() );
);
故点M坐标为(﹣![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
-
科目: 来源: 题型:
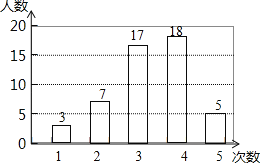
查看答案和解析>>【题目】在开展“学雷锋社会实践”活动中,某校为了解全校1000名学生参加活动的情况,随机调查了50名学生每人参加活动的次数,并根据数据绘成如图的条形统计图:
(1)这50个样本数据的中位数是 次,众数是 次;
(2)求这50个样本数据的平均数;
(3)根据样本数据,估算该校1000名学生大约有多少人参加了4次实践活动.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地如图,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数图象;折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数图象;请根据图象解答下到问题:
(1)货车离甲地距离y(干米)与时间x(小时)之间的函数式为 ;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在平面直角坐标系中A(5,0),B为y轴上任意一点,以点B为直角顶点作等腰Rt△ABC(点A、B、C按顺时针方向排列),请探究点C是否在一确定的直线上;
(2)在平面直角坐标系中,A(﹣1,0),B(4,2m),连接AB,将AB绕点B逆时针旋转90°到CB,请探究点C是否在一确定的直线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数
人数
班级
60
70
80
90
100
1班
0
1
6
2
1
2班
1
1
3
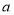
1
3班
1
1
4
2
2
分析数据:
平均数
中位数
众数
1班
83
80
80
2班
83
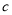
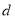
3班
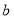
80
80
根据以上信息回答下列问题:
(1)请直接写出表格中
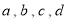 的值;
的值;(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级新生共570人,试估计需要准备多少张奖状?
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。
(1)将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进
 、
、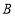 两种粽子1100个,购买
两种粽子1100个,购买 种粽子与购买
种粽子与购买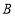 种粽子的费用相同,已知
种粽子的费用相同,已知 粽子的单价是
粽子的单价是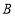 种粽子单价的1.2倍.
种粽子单价的1.2倍.(1)求
 、
、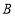 两种粽子的单价各是多少?
两种粽子的单价各是多少?(2)若计划用不超过7000元的资金再次购买
 、
、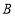 两种粽子共2600个,已知
两种粽子共2600个,已知 、
、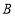 两种粽子的进价不变,求
两种粽子的进价不变,求 中粽子最多能购进多少个?
中粽子最多能购进多少个?
相关试题

