【题目】一家公司招考员工,每位考生要在A,B,C,D,E这5道试题中谁家抽出2道题回答,规定答对其中1题即为合格.
(1)请用树状图表示出所有可能的出题情形;
(2)已知某位考生只会答A,B两题,试求这位考生合格的概率.
参考答案:
【答案】
(1)解:列表得:
(A,E) | (B,E) | (C,E) | (D,E) | ﹣ |
(A,D) | (B,D) | (C,D) | ﹣ | (E,D) |
(A,C) | (B,C) | ﹣ | (D,C) | (E,C) |
(A,B) | ﹣ | (C,B) | (D,B) | (E,B) |
﹣ | (B,A) | (C,A) | (D,A) | (E,A) |
(2)解:由表格可知共有20种可能的情况,其中合格的结果有14个,所以P(这位考生合格)= ![]()
【解析】(1)首先根据题意列出表格或画树状图即可得出所有可能的出题情形;(2)然后由表格求得所有等可能的结果与某位考生只会答A,B两题的情况,再利用概率公式即可求得答案.
【考点精析】掌握列表法与树状图法是解答本题的根本,需要知道当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,点 E、F分别为边 AD、CD上的动点(都与菱形的顶点不重合),联结 EF、BE、BF .
(1)若∠A=60°,且 AE+CF=AB,判断△BEF 的形状,并说明理由;
(2)在(1)的条件下,设菱形的边长为a,求△BEF面积的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各多少万元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元. 则有哪几种购车方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形ABCD,点M,N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE.求证:
(1)∠DFM=∠BEN;
(2)四边形MENF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,…….照此规律,点P第100次跳动至点P100的坐标是( )

A. (-26,50) B. (-25,50) C. (26,50) D. (25,50)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
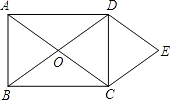
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
相关试题

