【题目】如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°.求:∠DCE和∠DCA的度数. 
请将以下解答补充完整,
解:因为∠DAB+∠D=180°
所以DC∥AB()
所以∠DCE=∠B()
又因为∠B=95°,
所以∠DCE=°;
因为AC平分∠DAB,∠CAD=25°,根据角平分线定义,
所以∠CAB==°,
因为DC∥AB
所以∠DCA=∠CAB,()
所以∠DCA=°.
参考答案:
【答案】同旁内角互补,两直线平行;两直线平行,同位角相等;95;∠CAD;25;两直线平行,内错角相等;25
【解析】解:∵∠DAB+∠D=180°,
∴DC∥AB(同旁内角互补,两直线平行),
∴∠DCE=∠B(两直线平行,同位角相等).
又∵∠B=95°,
∴∠DCE=95°;
∵AC平分∠DAB,∠CAD=25°,
∴∠CAB=∠CAD=25°,
∵DC∥AB
∴∠DCA=∠CAB,(两直线平行,内错角相等),
∴∠DCA=25°.
所以答案是:同旁内角互补,两直线平行;两直线平行,同位角相等;95;∠CAD,25;两直线平行,内错角相等;25.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a﹣b=3,那么12a2﹣8ab+b2﹣12a+3的值为( )
A. 9 B. 12 C. 15 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,则下列结论:①CF=AE;②OE=OF;③DE=BF;④图中共有四对全等三角形.其中正确结论的个数是( )
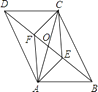
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是线段AB和线段CD的中点.
(1)求证:△AOD≌△BOC;
(2)求证:AD∥BC.
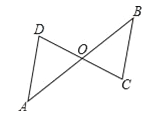
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.
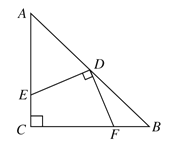
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题:
在某场CBA比赛中,某位运动员的技术统计如下表所示:
技术
上场时间(分钟)
出手投篮(次)
投中
(次)
罚球得分(分)
篮板
(个)
助攻(次)
个人总得分(分)
数据
38
27
11
6
3
4
33
注:(1)表中出手投篮次数和投中次数均不包括罚球;
(2)总得分=两分球得分+三分球得分+罚球得分.
根据以上信息,求本场比赛中该运动员投中两分球和三分球各几个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一问题中,自变量是________.
相关试题

