【题目】综合与探究
数学课上,老师让同学们利用三角形纸片进行操作活动,探究有关线段之间的关系.
问题情境:
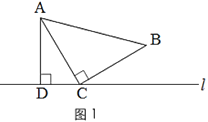
如图1,三角形纸片ABC中,∠ACB=90°,AC=BC.将点C放在直线l上,点A,B位于直线l的同侧,过点A作AD⊥l于点D.
初步探究:
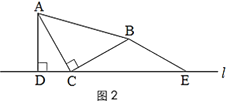
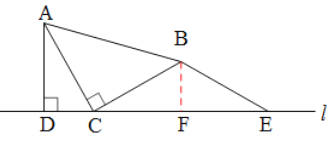
(1)在图1的直线l上取点E,使BE=BC,得到图2.猜想线段CE与AD的数量关系,并说明理由;
变式拓展:
(2)小颖又拿了一张三角形纸片MPN继续进行拼图操作,其中∠MPN=90°,MP=NP.小颖在图 1 的基础上,将三角形纸片MPN的顶点P放在直线l上,点M与点B重合,过点N作NH⊥l于点 H.
请从下面 A,B 两题中任选一题作答,我选择_____题.
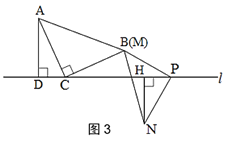
A.如图3,当点N与点M在直线l的异侧时,探究此时线段CP,AD,NH之间的数量关系,并说明理由.
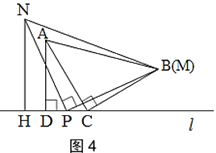
B.如图4,当点N与点M在直线l的同侧,且点P在线段CD的中点时,探究此时线段CD,AD,NH之间的数量关系,并说明理由.
参考答案:
【答案】(1)CE=2AD;(2)A题:CP=AD+NH;B题:NH=![]() CD+AD.
CD+AD.
【解析】
(1) 过点B作BF⊥l于点F,通过已知条件证得△ACD≌△CBF,再通过等腰三角形性质即可求解.
(2) ①过点B作BF⊥l于点F,通过已知条件△ACD≌△CBF证得△BFP≌△PHN,即可得出边边之间关系.
②过点B作BF⊥l于点F,通过已知条件△ACD≌△CBF证得△BFP≌△PHN,再通过边边转化即可求解.
(1)CE=2AD,理由如下:
过点B作BF⊥l于点F,易得∠CFB=90°
∵AD⊥l
∴∠ADC=90°,∠CAD+∠DCA=90°
∴∠ADC=∠CFB
∵∠ACB=90°
∴∠DCA+∠BCF=90°
∴∠CAD=∠BCF
在△ACD和△CBF 中
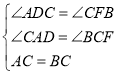
∴△ACD≌△CBF(AAS)
∴AD=CF
∵BE=BC,BF⊥l
∴CF=EF
∴CE=2CF=2AD
(2)A.CP=AD+NH,理由如下:
过点B作BF⊥l于点F,易得∠BFP=90°,
由(1)可得:△ACD≌△CBF
∴AD=CF
∵NH⊥l
∴∠PHN=90°,∠HNP+∠HPN=90°
∴∠BFP=∠PHN
∵∠MPN=90°
∴∠HPN+∠FPB=90°
∴∠HNP=∠FPB
在△BFP和△PHN 中
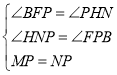
∴△BFP≌△PHN(AAS)
∴NH=PF
∵CP=CF+PF
∴CP=AD+NH
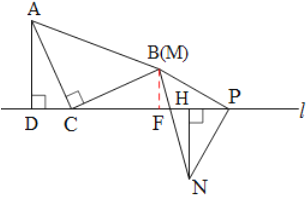
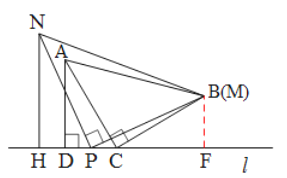
B.NH=![]() CD+AD,理由如下:
CD+AD,理由如下:
过点B作BF⊥l于点F,易得∠BFC=90°,
由(1)可得:△ACD≌△CBF
∴AD=CF
∵NH⊥l
∴∠PHN=90°,∠HNP+∠HPN=90°
∴∠BFP=∠PHN
∵∠MPN=90°
∴∠HPN+∠FPB=90°
∴∠HNP=∠FPB
在△BFP 和△PHN中
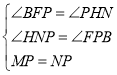
∴△BFP≌△PHN(AAS)
∴NH=PF
∵点P在线段CD的中点
∴CP=DP=![]() CD
CD
由图得:PF=PC+CF
∴NH=![]() CD+AD
CD+AD
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图:

(1)如图甲,以点O为中心,把点P顺时针旋转45°;
(2)如图乙,以点O为中心,把线段AB逆时针旋转90°;
(3)如图丙,以点O为中心,把△ABC顺时针旋转120°;
(4)如图丁,以点B为中心,把△ABC旋转180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图 1,O 是等边三角形 ABC 内一点,连接 OA,OB,OC,且 OA=3,OB=4,OC=5,将△BAO 绕点 B 顺时针旋转后得到△BCD,连接 OD.
填空:①旋转角为 °;②线段 OD 的长是 ;③∠BDC= °;
(2)如图 2,O 是△ABC 内一点,且∠ABC=90°,BA=BC. 连接 OA,OB,OC,将△BAO 绕点 B 顺时针旋转后得到△BCD,连接 OD.当 OA,OB,OC 满足什么条件时,∠BDC=135°?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长分别为a,b的两个正方形并排放在一起,请计算图中阴影部分面积,并求出当a+b=16,ab=60时阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L,M,D在AK的同旁,连接BK和DM,试用旋转的思想说明线段BK与DM的关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格中每个小正方形的边长为1,点C(0,1),点B(-1,3).
(1)利用网格画出直角坐标系(要求标出x轴,y轴和原点),则点A的坐标为_________;
(2)以△ABC为基本图形,利用旋转设计一个图案,说明你的创意为__________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

相关试题

