【题目】(1)如图 1,O 是等边三角形 ABC 内一点,连接 OA,OB,OC,且 OA=3,OB=4,OC=5,将△BAO 绕点 B 顺时针旋转后得到△BCD,连接 OD.
填空:①旋转角为 °;②线段 OD 的长是 ;③∠BDC= °;
(2)如图 2,O 是△ABC 内一点,且∠ABC=90°,BA=BC. 连接 OA,OB,OC,将△BAO 绕点 B 顺时针旋转后得到△BCD,连接 OD.当 OA,OB,OC 满足什么条件时,∠BDC=135°?请说明理由.

参考答案:
【答案】(1)①60;②4;③150;(2) ![]() ,理由见解析
,理由见解析
【解析】
(1)根据△ABC是等边三角形可得旋转角为60°,根据旋转可得CD= OA=3,△B OD是等边三角形,即可求出OD 的长,再根据勾股定理逆定理求出∠ODC=90°即可求解;
(2)先根据△BAO 绕点 B 顺时针旋转后得到△BCD,可得∠OBD=∠ABC=90°,BO=BD,CD=AO,故得到△OBD是等腰直角三角形,DO=![]() ,再由勾股定理得到△OCD是直角三角形,∠ODC=90°,即OA2+2OB2=OC2,再进行等量替换即可求解.
,再由勾股定理得到△OCD是直角三角形,∠ODC=90°,即OA2+2OB2=OC2,再进行等量替换即可求解.
(1)①∵△ABC是等边三角形
∴BA=BC,∠ABC=60°
∵将△BAO 绕点 B 顺时针旋转后得到△BCD,
∴∠OBD=∠ABC=60°
∴旋转角为60°,
②∵将△BAO 绕点 B 顺时针旋转后得到△BCD,
∴BO= BD
∵∠OBD=60°
∴△B OD是等边三角形,
∴OD = OB=4,
③∵△B OD是等边三角形,
∴∠BDO=60°
∵将△BAO 绕点 B 顺时针旋转后得到△BCD,
∴CD= AO=3
在△OCD中,CD=3,OD=4,OC=5
∴CD2+OD2=OC2
∴△OCD是直角三角形,∠ODC=90°
∴∠BDC=∠BDO+∠ODC=150°
故答案为:①60;②4;③150;
(2)当OA2+2OB2=OC2时,∠BDC=135°,
理由如下:
∵将△BAO 绕点 B 顺时针旋转后得到△BCD,
∴∠OBD=∠ABC=90°,BO=BD,CD=AO
∴△OBD是等腰直角三角形,且∠BDO=45°,
∴DO=![]()
∵CD2+OD2=OC2时,△OCD是直角三角形,∠ODC=90°,
即当OA2+2OB2=OC2时,∠ODC=90°,∠BDC=135°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)
 ;(2)
;(2)  ;(3)
;(3)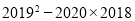 ; (4)
; (4) .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某地,人们发现在一定温度下某种蟋蟀叫的次数与温度之间有如下的竟是关系:

(1)在这个变化过程中,自变量是 ,因变量是 ;
(2)在当地温度
 每增加
每增加 ,这种蟋蟀
,这种蟋蟀 叫的次数
叫的次数 是怎样变化的?
是怎样变化的?(3)这种蟋蟀
 叫的次数
叫的次数 (次)与当地温度
(次)与当地温度 之间的关系为 ;
之间的关系为 ;(4)当这种蟋蟀
 叫的次数
叫的次数 时,求当时该地的温度.
时,求当时该地的温度. -
科目: 来源: 题型:
查看答案和解析>>【题目】作图:

(1)如图甲,以点O为中心,把点P顺时针旋转45°;
(2)如图乙,以点O为中心,把线段AB逆时针旋转90°;
(3)如图丙,以点O为中心,把△ABC顺时针旋转120°;
(4)如图丁,以点B为中心,把△ABC旋转180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长分别为a,b的两个正方形并排放在一起,请计算图中阴影部分面积,并求出当a+b=16,ab=60时阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
数学课上,老师让同学们利用三角形纸片进行操作活动,探究有关线段之间的关系.
问题情境:
如图1,三角形纸片ABC中,∠ACB=90°,AC=BC.将点C放在直线l上,点A,B位于直线l的同侧,过点A作AD⊥l于点D.
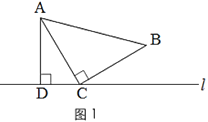
初步探究:
(1)在图1的直线l上取点E,使BE=BC,得到图2.猜想线段CE与AD的数量关系,并说明理由;
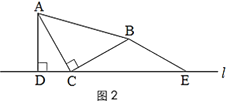
变式拓展:
(2)小颖又拿了一张三角形纸片MPN继续进行拼图操作,其中∠MPN=90°,MP=NP.小颖在图 1 的基础上,将三角形纸片MPN的顶点P放在直线l上,点M与点B重合,过点N作NH⊥l于点 H.
请从下面 A,B 两题中任选一题作答,我选择_____题.
A.如图3,当点N与点M在直线l的异侧时,探究此时线段CP,AD,NH之间的数量关系,并说明理由.
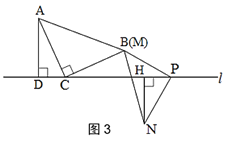
B.如图4,当点N与点M在直线l的同侧,且点P在线段CD的中点时,探究此时线段CD,AD,NH之间的数量关系,并说明理由.
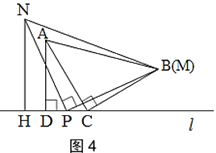
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L,M,D在AK的同旁,连接BK和DM,试用旋转的思想说明线段BK与DM的关系.

相关试题

