【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

参考答案:
【答案】(1)∠DBC=30°;(2)BC=8.
【解析】
(1)由在△ABC中,AB=AC,∠A=40°,利用等腰三角形的性质,即可求得∠ABC的度数,然后由AB的垂直平分线MN交AC于点D,根据线段垂直平分线的性质,可求得AD=BD,继而求得∠ABD的度数,则可求得∠DBC的度数.
(2)根据AE=6,AB=AC,得出CD+AD=12,由△CBD的周长为20,代入即可求出答案.
解:(1)∵在△ABC中,AB=AC,∠A=40°,
∴∠ABC=∠C=70°
∵AB的垂直平分线MN交AC于点D,
∴AD=BD,
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC-∠ABD=30°
(2)∵AE=6,
∴AC=AB=2AE=12
∵△CBD的周长为20,
∴BC=20-(CD+BD)=20-(CD+AD)=20-12=8,
∴BC=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
数学课上,老师让同学们利用三角形纸片进行操作活动,探究有关线段之间的关系.
问题情境:
如图1,三角形纸片ABC中,∠ACB=90°,AC=BC.将点C放在直线l上,点A,B位于直线l的同侧,过点A作AD⊥l于点D.
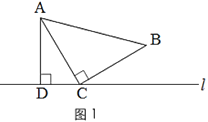
初步探究:
(1)在图1的直线l上取点E,使BE=BC,得到图2.猜想线段CE与AD的数量关系,并说明理由;
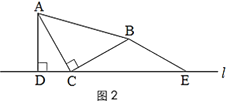
变式拓展:
(2)小颖又拿了一张三角形纸片MPN继续进行拼图操作,其中∠MPN=90°,MP=NP.小颖在图 1 的基础上,将三角形纸片MPN的顶点P放在直线l上,点M与点B重合,过点N作NH⊥l于点 H.
请从下面 A,B 两题中任选一题作答,我选择_____题.
A.如图3,当点N与点M在直线l的异侧时,探究此时线段CP,AD,NH之间的数量关系,并说明理由.
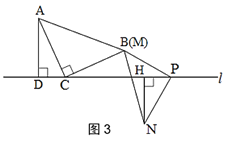
B.如图4,当点N与点M在直线l的同侧,且点P在线段CD的中点时,探究此时线段CD,AD,NH之间的数量关系,并说明理由.
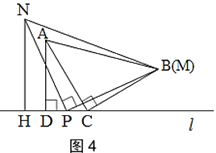
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L,M,D在AK的同旁,连接BK和DM,试用旋转的思想说明线段BK与DM的关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格中每个小正方形的边长为1,点C(0,1),点B(-1,3).
(1)利用网格画出直角坐标系(要求标出x轴,y轴和原点),则点A的坐标为_________;
(2)以△ABC为基本图形,利用旋转设计一个图案,说明你的创意为__________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的
 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用直接开平方法解方程:
(1) 4(x-2)2-36=0;
(2) x2+6x+9=25;
(3) 4(3x-1)2-9(3x+1)2=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
相关试题

