搜索
【题目】已知，如图，点A、D、B、E在同一直线上，AC=EF,AD=BE，∠A=∠E，
（1）求证：△ABC≌△EDF；
（2）当∠CHD=120°，猜想△HDB的形状，并说明理由．
参考答案：
【答案】（1）见解析；（2）△HDB为等边三角形；理由见解析；
【解析】
（1）根据SAS即可证明：△ABC≌△EDF；
（2）由（1）可知∠HDB=∠HBD，再利用三角形的外角关系即可得三角形HDB为等边三角形．
(1)证明：
∵AD=BE，
∴AD+DB=BE+DB,
∴AB=ED，
在△ABC和△EDF中，
,
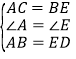∴△ABC≌△EDF（SAS）；
(2) △HDB为等边三角形，理由如下：
∵△ABC≌△EDF，
∴∠HDB=∠HBD，
∵∠CHD=∠HDB+∠HBD=120°，
∴∠HDB=∠HBD=60°，
∠DHB=60°．
∴△HDB为等边三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某农庄计划在30亩空地上全部种植蔬菜和水果，菜农小张和果农小李分别承包了种植蔬菜和水果的任务．小张种植每亩蔬菜的工资y（元）与种植面积m（亩）之间的函数如图①所示，小李种植水果所得报酬z（元）与种植面积n（亩）之间函数关系如图②所示．
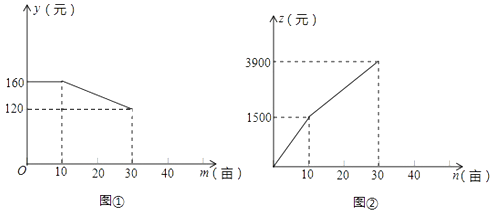
（1）如果种植蔬菜20亩，则小张种植每亩蔬菜的工资是元，小张应得的工资总额是元，此时，小李种植水果亩，小李应得的报酬是元；
（2）当10＜n≤30时，求z与n之间的函数关系式；
（3）设农庄支付给小张和小李的总费用为w（元），当10＜m≤30时，求w与m之间的函数关系式． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图：长方形ABCD中，AD=10，AB=4，点Q是BC的中点，点P在AD边上运动，当△BPQ是等腰三角形时，AP的长为 .
-
科目： 来源： 题型：
查看答案和解析>>【题目】等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连接AF，BE相交于点P．
（1）若AE=CF； ①求证：AF=BE，并求∠APB的度数；
②若AE=2，试求APAF的值；
（2）若AF=BE，当点E从点A运动到点C时，试求点P经过的路径长． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=10cm，BC=6cm，AC=8cm，BD是∠ABC的角平分线。
（1）求△ABC的面积；
（2）求△ABC的角平分线BD的长；
（3）若点E是线段AB上的一个动点，从点B以每秒2cm的速度向A运动，几秒种后△EAD是直角三角形？（此小题可直接写出答案）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在长方形ABCD中,AB=4，AD=6.延长BC到点E，使CE=2,连接DE,动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为（ ）秒时，△ABP和△DCE全等．
A. 1 B. 1或3 C. 1或7 D. 3或7
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：如图1，等腰△ABC中，点E，F分别在腰AB，AC上，连结EF，若AE＝CF，则称EF为该等腰三角形的逆等线．
（1）如图1，EF是等腰△ABC的逆等线，若EF⊥AB，AB＝AC＝5，AE ＝2，求逆等线EF的长；
（2）如图2，若等腰直角△DEF的直角顶点D恰好为等腰直角△ABC底边BC上的中点，且点E，F分别在AB，AC上，求证：EF为等腰△ABC的逆等线；
（3）如图3，边长为6的等边三角形△AOC的边OC与X轴重合，EF是该等边三角形的逆等线．F点的坐标为（5，
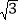）；试求点E的坐标(若需要，本题可以直接应用结论：在直角三角形中，30°角所对的直角边等于斜边的一半．)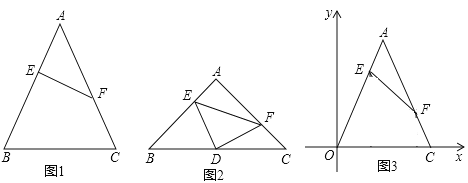
相关试题
