Question

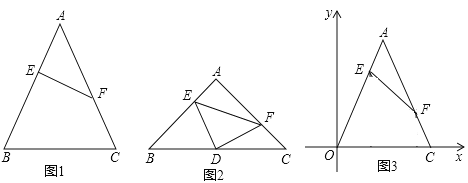
【题目】定义：如图1，等腰△ABC中，点E，F分别在腰AB，AC上，连结EF，若AE＝CF，则称EF为该等腰三角形的逆等线．

（1）如图1，EF是等腰△ABC的逆等线，若EF⊥AB，AB＝AC＝5，AE ＝2，求逆等线EF的长；

（2）如图2，若等腰直角△DEF的直角顶点D恰好为等腰直角△ABC底边BC上的中点，且点E，F分别在AB，AC上，求证：EF为等腰△ABC的逆等线；

（3）如图3，边长为6的等边三角形△AOC的边OC与X轴重合，EF是该等边三角形的逆等线．F点的坐标为（5，）；试求点E的坐标(若需要，本题可以直接应用结论：在直角三角形中，30°角所对的直角边等于斜边的一半．)

Answer 1

【答案】（1） （2）见解析 （3）E（2，）

【解析】

（1）由逆等线的性质可求得CF和AE，由条件可求得AF，在Rt△AEF中，由勾股定理可求得EF的长；
（2）连接AD，可证明△EDA≌△FDC，可求得AE=CF，可证得结论；
（3）过E、F分别作EG⊥OC于G , FH⊥OC于H，由勾股定理可得FC，由逆等线知AE=2，在△OEG中，分别求得OG、EG即可得点E的坐标.

解：
（1）∵EF是等腰△ABC的逆等线，
∴CF=AE=2，又AB=AC=5，
∴AF=3，
∵EF⊥AB，
∴EF= = ，

（2）连结AD，在等腰Rt△ABC中，点D为底边上中点，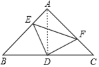

∴AD=CD且∠ADC=90°，
又∵DE=DF且∠EDF=90°，
∴∠EDA=90°-∠ADF=∠FDC，
在△EDA和△FDC中，

,

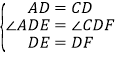∴△EDA≌△FDC（SAS），
∴AE=CF，
∴EF为等腰△ABC的逆等线；

(3)过E、F分别作EG⊥OC于G , FH⊥OC于H，

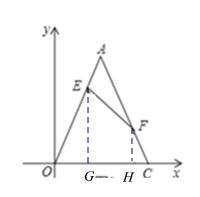
∵F点的坐标为（5，），

∴FH=,OH=5，

则HC=OC-OH=6-5=1,

在Rt△FHC中，FC= ,

∴AE=FC=2,

∴OE=OA-AE=6-2=4,

又∵FH⊥OC，∠AOC=60°，

∴∠OEG=30°，

∴OG=OE=2,( 在直角三角形中，30°角所对的直角边等于斜边的一半)

∴EG= = = ,

∴E（2，）.